CHAPTER 6 – PHÂN TÍCH HỒI QUY
Cung cấp một cái nhìn tổng quan về cách sử dụng kết quả phân tích hồi quy, bao gồm: Ước tính chi phí biến đổi và chi phí cố định Xây dựng phương trình chi phí để dự báo một loạt chi phí trong tương lai....
I. Mục tiêu
● Thể hiện sự hiểu biết về một phương trình hồi quy đơn giản (a simple regression equation)
● Xác định một phương trình hồi quy bội (multiple regression equation) và nhận biết khi nào hồi quy bội là một công cụ thích hợp (appropriate) để sử dụng để dự báo (forecasting)
● Tính toán kết quả (result) của một phương trình hồi quy đơn giản.
II. Nội dung
Cung cấp một cái nhìn tổng quan về cách sử dụng kết quả phân tích hồi quy, bao gồm:
➢ Ước tính chi phí biến đổi và chi phí cố định
➢ Xây dựng phương trình chi phí để dự báo một loạt chi phí trong tương lai
1. Hồi quy đơn biến (Simple regression)
a. Định nghĩa:
Phân tích hồi quy là quá trình rút ra phương trình tuyến tính (deriving the linear equation) mô tả mối quan hệ giữa hai biến có hệ số tương quan khác không (two variables with a non-zero coefficient of correlation). Nó là một công cụ thống kê được sử dụng để làm nổi bật các mẫu dữ liệu thống kê trong dữ liệu lịch sử.
b. Cách ghi nhận
Phương trình hồi quy đơn biến là phương trình đại số biểu diễn dưới dạng một đường thẳng:
y = a + bx
*Trong đó:
y = Biến phụ thuộc
a = Giao tuyến y
b = Độ dốc của đường hồi quy (the slope of the regression line)
x = Biến độc lập
c. Ví dụ:
Một ví dụ về bảng chi phí có thể được trình bày như dưới đây:
|
Quý |
Bảng |
Chi phí |
|
1 |
106 |
$112,300 |
|
2 |
125 |
$176,750 |
|
3 |
183 |
$161,000 |
|
4 |
249 |
$212,125 |
|
5 |
213 |
$224,300 |
|
6 |
155 |
$236,360 |
|
7 |
130 |
$107,800 |
|
8 |
170 |
$239,500 |
Dựa trên kết quả được tạo bởi công cụ phân tích,
Tổng chi phí = $702 (ô tô) + $65,079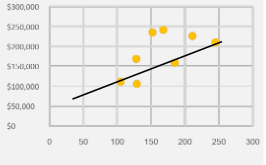
*Lưu ý: Phép Hồi quy đơn sau khi có được bảng số chi tiết thì được chia làm 2 loại kết quả , bao gồm: Ý nghĩa thống kê (Statistical significance) và Ý nghĩa thực tiễn (Practical significance).
- Ý nghĩa thống kê (Statistical significance):
Ý nghĩa thống kê đề cập đến tuyên bố rằng (claim) kết quả từ dữ liệu được tạo ra (data generated) bằng thử nghiệm hoặc thí nghiệm (testing or experimentation) có khả năng được quy (attributable) cho một nguyên nhân cụ thể.
Ví dụ: Dựa vào dữ liệu ở ví dụ 1, sử dụng công cụ phân tích hồi quy trong Excel, ta có bảng ý nghĩa thống kê của các dự toán:
|
Hệ số tương quan |
Sai số chuẩn |
Thống kê kiểm định |
Trị số P |
Thấp hơn 95% |
Vượt 95% |
Thấp hơn 80% |
Vượt 80% |
|
|
Giao điểm |
$65,079 |
$63,222 |
1.03 |
0.34 |
($91,585) |
$223,683 |
($26,702) |
$158,801 |
|
Số lượng ô tô sản xuất |
$702 |
$377 |
1.87 |
0.11 |
($219) |
$1,624 |
$160 |
$1,245 |
- Ý nghĩa thực tiễn (Practical significance):Ý nghĩa thực tế đề cập đến độ lớn của sự khác biệt (magnitude of the difference), được gọi là kích thước hiệu ứng (effect size). Kết quả thực tế có ý nghĩa khi sự khác biệt đủ lớn để có ý nghĩa trong cuộc sống thực (meaningful in real life).
Dựa vào dữ liệu ở ví dụ 1, sử dụng công cụ phân tích hồi quy (regression analysis tools)trong Excel, ta có bảng ý nghĩa thực tế (Practical significance) của phương trình tổng chi phí cho nhà sản xuất bo mạch.
|
Bội số R |
0.61 |
|
R bình phương |
0.37 |
|
R bình phương hiệu chỉnh |
0.26 |
|
Sai số chuẩn |
$47,655 |
|
Kỹ thuật quan sát |
8 |
2. Hồi quy bội (Multiple regression)
a. Định nghĩa:
Hồi quy bội (multiple regression) được sử dụng khi có nhiều hơn một biến độc lập (more than one independent variables).
Hồi quy bội cho phép công ty xác định nhiều yếu tố thay vì chỉ một biến độc lập và cân nhắc từng yếu tố theo ảnh hưởng của nó đối với kết quả chung, do đó làm tăng độ chính xác của dự báo.
b. Cách ghi nhận:
Phương trình hồi quy bội:
y = a + b1x1 + b2x2 + … + bnxn
*Trong đó:
y = Biến phụ thuộc
a = Giao tuyến y
b = Độ dốc của đường hồi quy (the slope of the regression line)
x = Biến độc lập
c. Ví dụ:
Những dữ liệu này đại diện cho 24 học kỳ hoạt động và chi phí cho một trường đại học:
|
Học kỳ |
Sinh viên đã đăng ký |
Phần giảng dạy |
Các khóa học được liệt kê |
Tổng chi phí đại học |
|
Mùa thu 06 |
28,874 |
7,065 |
2,670 |
$117,160,456 |
|
Xuân 07 |
29,091 |
6,775 |
2,670 |
$117,352,268 |
|
Mùa thu 07 |
28,621 |
6,232 |
2,628 |
$115,928,777 |
|
Mùa xuân 08 |
27,310 |
6,833 |
2,678 |
$116,889,599 |
|
: |
: |
: |
: |
: |
|
Mùa thu 16 |
29,374 |
7,521 |
3,030 |
$127,352,245 |
|
Mùa xuân 17 |
32,227 |
7,258 |
2,820 |
$128,577,777 |
|
Mùa thu 17 |
31,263 |
7,249 |
2,817 |
$128,408,000 |
|
Mùa xuân 18 |
29,197 |
7,142 |
2,876 |
$129,436,179 |
Sử dụng công cụ phân tích hồi quy trong Excel™, phân tích hồi quy bội của dữ liệu ở trên được cung cấp bên dưới.
Yêu cầu: Phương trình tổng chi phí cho trường đại học là gì và bao nhiêu phương sai chi phí đang được giải thích?
|
Hệ số tương quan |
Sai số chuẩn |
Thống kê kiểm định |
Trị số P |
Thấp hơn 95% |
Vượt 95% |
Thấp hơn 80% |
Vượt 80% |
|
|
Giao điểm |
$19,464,902 |
$18,869,075 |
1.03 |
0.31 |
($19,895,299) |
$58,825,103 |
($5,543,051) |
$44,472,855 |
|
Sinh viên đã đăng ký |
$1,045 |
$596 |
1.75 |
0.09 |
($198) |
$2,287 |
$255 |
$1,834 |
|
Phần giảng dạy |
$4,159 |
$1,451 |
2.87 |
0.01 |
$1,132 |
$7,186 |
$2,236 |
$6,082 |
|
Các khóa học được liệt kê |
$15,778 |
$5,529 |
2.85 |
0.01 |
$4,245 |
$27,311 |
$8,451 |
$23,106 |
|
Bội số R |
0.83 |
|
R bình phương |
0.68 |
|
R bình phương hiệu chỉnh |
0.64 |
|
Sai số chuẩn |
$2,698,662 |
|
Kỹ thuật quan sát |
24 |
Hướng dẫn giải:
Dựa trên các Hệ số (Coefficients) được hiển thị (displayed) trong cột đầu tiên ở trên, phương trình tổng chi phí (cost equation) cho trường đại học là:
Tổng chi phí = $1,045 (Sinh viên) + $4,159 (Phần) + $15,778 (Khóa học) + $19,464,902
Đối với chi phí cố định: ước tính tổng chi phí cố định (Giá trị chặn-(the Intercept) hoàn toàn không chính xác (not at all precise);
lỗi tiêu chuẩn ($18,869,075) lớn gần bằng chính ước tính chi phí ($19,464,902).
Chỉ số t cho chi phí cố (t-Stat for fixed costs) định nhỏ hơn nhiều so với 2 (trong đó trạng thái t tốt hơn là > 3) giá trị P lớn hơn nhiều 0,10 (trong đó giá trị p tốt hơn là < 0,05) khoảng tin cậy (confidence intervals) ở cả hai 95% và 80% đang đi vào phạm vi tiêu cực.
Đối với chi phí biến đổi: ước tính cho 3 biến tốt hơn, đa số các biến có chỉ số t cao hơn nhiều so với 2, ngoại trừ số lượng sinh viên theo học, giá trị P đều thấp hơn 0,1 khoảng tin cậy ở cả 95% và 80% đều không vượt quá phạm vi âm (negative range).
Ý nghĩa thực tiễn:
Với thống kê R Square (Adjusted R Square) đã điều chỉnh là 0,64, ước tính chi phí (cost estimates) trong phân tích đang giải thích 64% phương sai trong tổng chi phí trong tập dữ liệu.
Cuối cùng, các nhà quản lý có thể sử dụng Sai số Chuẩn (Standard Error) ($2,698,662) để dự đoán tổng chi phí. Ví dụ: nếu ngân sách của trường đại học được lên kế hoạch trong học kỳ tới cho 29.500 sinh viên theo học, để dạy 7.100 phần và có 2.800 khóa học dành cho sinh viên, phương trình tổng chi phí sẽ là:
Tổng chi phí = $1.045 ( 29.500 ) + $4.159 ( 7.100 ) + $15.778 ( 2.800 ) + $19.464.902 = $123.999.702
Người quản lý có thể tự tin khoảng 68% khi dự báo (approximately 68% confident in forecasting) rằng chi phí thực tế nằm trong khoảng từ $121.301.040 đến $126.698.364 ( = $123.999.702 ± $2.698.662)
III. Bài tập
Example 1 for Simple Regression:
A manufacturing company incurs $500,000 in fixed costs per year, and variable costs per unit are $10. The company plans to produce 300,000 units next year.
Assuming that fixed and variable costs per unit remain constant, what is the expected total cost of production next year?
Answer:
The relevant values are as follows:
Fixed costs: a = $500,000
Variable cost per unit: B = $10
Production/output: x = 300,000 units
These values shown are substituted into the simple regression equation:
y (total cost) = $500,000+ ($10 per unit x 300,000 units) = $3,500,000
The total cost is driven by the level of production activity as the sole independent variable. As production changes, projected total costs will increase or decrease commensurately.
Example 2 for Multiple Regression:
An international not-for-profit organization finances medical research. The majority of its revenue and support comes from fundraising activities, investments, and specific grants from an initial sponsoring corporation. The organization has been in operation for over 15 years and has just finished a major fundraising event that raised $500 million for the current fiscal period.
The following are selected data from recent financial statements (in millions of dollars).
|
Current Year |
Past Year |
|
|
Revenue |
$500 |
$425 |
|
Investments(average balances) |
210 |
185 |
|
Investment income |
16 |
20 |
|
Administrative expense |
10 |
8 |
A financial analyst wants to determine whether the change in investment income during the current year was due to changes in investment strategy, changes in portfolio mix, or other factors.
Require: Which one of the following techniques should be used?
A. Ratio analysis that compares changes in the investment portfolio monthly.
B. Multiple regression analysis that includes independent variables associated with the nature of the investment portfolio and market conditions.
C. Best-practice analysis that compares the investment income as a percentage of total assets with a competitor's investment income as a percentage of total assets.
D. Simple linear regression that compares investment income changes over the past five years to determine the nature of the changes.
Answer:
Choice "B" is correct. A critical component of financial analysis is examining results over time to see where changes have occurred, and then develop an understanding of the drivers behind those changes.
Merely looking at the numbers rarely tells the story; therefore, a more detailed analysis is needed to provide context to the numbers and to help others understand the underlying drivers of change. Multiple linear regression is a statistical method used to model the relationship between one dependent (or response) variable and two or more independent (or explanatory) variables by developing a linear equation based on observed data. The purpose of doing so is to understand what independent factors are impacting the performance of the dependent variable.
Applying a multiple regression analysis here should allow the analyst to ascertain if the investment strategy, portfolio mix, or some other factor is the primary contributor to the change in investment income.