CHAPTER 7 – TÍNH TOÁN GIÁ TRỊ DỰ KIẾN VÀ PHÂN TÍCH ĐƯỜNG CONG LĨNH HỘI

Các phép toán về những dự kiến trong tương lai (future expectations), những công cụ này hữu ích hơn cho các nhà quản lý cho mục đích dự báo (forecasting purpose). Phân tích đường cong lĩnh hội (learning curve analysis)...

I.  Mục tiêu

• Tính giá trị dự kiến của các biến ngẫu nhiên
• Xác định những lợi ích và thiếu sót của các kỹ thuật tính giá trị dự kiến (expected value techniques)
• Sử dụng các giá trị xác suất để ước tính dòng tiền trong tương lai
• Thể hiện sự hiểu biết về phân tích đường cong lĩnh hội
• Tính toán kết quả theo mô hình học thời gian trung bình tích lũy (cumulative average-time)
• Liệt kê những lợi ích và thiếu sót (shortcomings) của phân tích hồi quy (regression analysis) và phân tích đường cong lĩnh hội (learning curve analysis)

II.  Nội dung

Trong bài học này, chúng ta sẽ tìm hiểu về hai công cụ, bao gồm:
➢    Các phép toán về những dự kiến trong tương lai (future expectations), những công cụ này hữu ích hơn cho các nhà quản lý cho mục đích dự báo (forecasting purpose). Các phép tính giá trị dự kiến (expected value techniques) kết hợp một số kết quả có thể xảy ra trong tương lai để dự đoán giá trị tương lai dự kiến của tất cả các kết quả có thể xảy ra. 
➢    Phân tích đường cong lĩnh hội (learning curve analysis) nắm bắt những cải tiến lĩnh hội (learning improvements) dự kiến trong các quy trình và chi phí của tổ chức để dự báo mức trung bình động của chi phí trong tương lai (a moving average of future costs).

1.   Các phép toán tính giá trị dự kiến (Expected Value Computations)

a.   Định nghĩa:
➢    Giá trị dự kiến (Expected Value (EV)) là giá trị trung bình có trọng số của các kết quả của một hành động trong đó giá trị của các kết quả có thể xảy ra được tính theo xác suất của chúng. Khi tồn tại nhiều kết quả tiềm ẩn, mỗi kết quả có một giá trị cùng với xác suất liên quan phải nằm trong khoảng từ 0% đến 100%, với tổng tất cả các xác suất bằng 100%. 
➢    Một ứng dụng khác có giá trị của phương pháp giá trị dự kiến là ước tính các dòng tiền trong tương lai.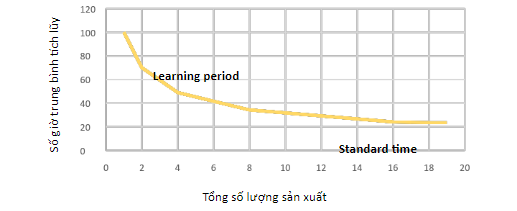 

b.   Công thức

Để tính toán giá trị dự kiến, mỗi giá trị được nhân với xác suất liên quan của nó và số tiền được cộng lại để tạo ra tổng giá trị dự kiến.

Ev=Σ(rp)

*Trong đó:
r = kết quả của đầu ra (outcome)
p = xác suất của đầu ra .
Ký hiệu Hy Lạp Σ đại diện cho "tổng hợp"

c.  Ví dụ:

Trong quy trình lập kế hoạch ngân sách, người ta ước tính rằng chi phí cố định trong năm tới cho một bộ phận sẽ là 100.000 đô la. Tuy nhiên, có 10% xác suất chi phí cố định có thể thấp tới 50.000 USD. Cũng có 20% xác suất rằng chi phí cố định sẽ cao tới 200.000 USD. Giá trị dự kiến của chi phí cố định trong năm tới sẽ được tính như sau:

Giải thích:

Tổng xác suất phải cộng lại bằng 100%. Do đó, nếu có 10% xác suất xảy ra Kết quả 2 và 20% xác suất xảy ra Kết quả 3, thì dự đoán ban đầu (Kết quả 1) phải có xác suất 70%.
Trong ví dụ trên, giá trị dự kiến của chi phí cố định trong năm tới là $115,000. Số tiền này thể hiện sự kết hợp hợp lý của các dự kiến quản lý và có thể được sử dụng làm dự báo cho năm tới.

Lưu ý những lợi ích và thiếu sót của các kỹ thuật giá trị dự kiến (expected value techniques):

2.   Phân tích đường cong lĩnh hội (Learning curve analysis)

a.  Định nghĩa:

Thuyết đường cong học tập (Learning curve theory) nghiên cứu về chi phí lao động và thời gian sản xuất khi mà lực lượng lao động được sử dụng để làm một sản phẩm mới và cải tiến hiệu quả thông qua quá trình học hỏi và tích lũy kinh nghiệm.
Thuyết này giả định là có hiện tượng học tập, đúc rút kinh nghiệm sau mỗi sản phẩm sản xuất giúp năng suất sản phẩm được nâng cao.

Từ đó, có 2 khái niệm xuất hiện:

➢    Tỷ lệ học tập (Learning rate): được thể hiện dưới dạng phần trăm (VD: 90%,80%)
➢    Hiệu quả học tập(Learning effect): là ảnh hưởng của quá trình tiếp thu kinh nghiệm làm việc đến năng suất lao động. 
=>Do đó, mỗi khi năng suất tăng gấp đôi, thì thời gian sản xuất trung bình từng sản phẩm sẽ giảm theo tỉ lệ learning rate.

b. Công thức:

Điều kiện áp dụng
Thuyết này được áp dụng khi sản phẩm thỏa mãn bất kỳ điều kiện nào sau đây:

➔    Được sản xuất bằng năng lực lao động là chính thay vì dựa vào máy móc, thiết bị
➔    Là sản phẩm mới (quá trình học tập không kéo dài vô thời hạn);
➔    Sản phẩm phức tạp, sản xuất số lượng nhỏ cho các đơn hàng đặc biệt.   

Bên cạnh đó, các phép toán tính giá trị dự kiến (Expected Value Computations) được chia làm hai phương pháp áp dụng phân tích đường cong học tập được sử dụng phổ biến, bao gồm:
➔    Mô hình học tập trung bình tích lũy (Cumulative average-time learning model)
➔    Mô hình học tập tăng dần theo đơn vị thời gian (Incremental unit-time learning model)

Công thức cho mô hình học tập thời gian trung bình tích lũy là:

Y = aXb

*Trong đó:
Y = trung bình tích lũy trên mỗi đơn vị(cumulative average per unit)
a = thời gian cần thiết cho đơn vị đầu tiên(time required for first unit)
X = số đơn vị tích lũy (cumulative number of units)
b =Trong đường cong học tập % ÷ ln 2 (learning curve % ÷ ln 2) 

c.   Ví dụ:
Sản phẩm ABC có learning curve là 80%. Doanh nghiệp hiện tại đã sản xuất xong 30 chiếc ABC. Chiếc ABC đầu tiên sản xuất mất 120 tiếng làm việc.

Hỏi thời gian cần thiết để sản xuất chiếc ABC số 31 là bao nhiêu tiếng?

Lời giải
Thời gian sản xuất chiếc ABC số 31 sẽ bằng tổng thời gian sản xuất 31 chiếc trừ đi tổng thời gian sản xuất 30 chiếc.

Để giải bài toán ta cần tìm hết các biến số cần thiết cho công thức Y = ax^b
b = log 0.8/log 2 = (0.3219281)
x = 30
a = 120
Thời gian trung bình để sản xuất mỗi sản phẩm khi sản xuất 30 chiếc:
Y(30) = 30^(-0.3219281) x 120 = 40.147 (tiếng/chiếc)

Tổng thời gian sản xuất 30 chiếc:
40.147 x 30 = 1,204.41 (tiếng)

Thời gian trung bình để sản xuất mỗi sản phẩm khi sản xuất 31 chiếc:
Y(31) = 31^(-0.3219281) x 120 = 39.726 (tiếng/chiếc)

Tổng thời gian sản xuất 31 chiếc
39.726 x 31 = 1,231.51 (tiếng)

Thời gian sản xuất chiếc ABC số 31 là: 1,231.51 – 1,204.41 = 27.1 (tiếng)

Đánh giá Learning curve:

III.  Bài tập

Question 1: Expected Value practice question:
The controller for a manufacturing company is interested in estimating cash inflows for April. She estimates the following amounts and associated probabilities for the month: 
➢    10% probability of collecting $12 million 
➢    30% probability of collecting $14 million 
➢    20% probability of collecting $15 million
➢    40% probability of collecting $17 million

Given the estimates above, calculate the expected cash inflows for April.

Answer:

The table shows how the expected value of 41 minutes is calculated. In equation form, the output will be:

30 minutes (20% ) + 40 minutes (50%) + 50 minutes (30%) = 41 minutes

Although the most likely scenario (50% likelihood) is a value of 40 minutes, the expected value is 41 minutes.


Question 2: Estimating Future Cash Flows practice question:
The controller for a manufacturing company is interested in estimating cash inflows for April. She estimates the following amounts and associated probabilities for the month: 
●    10% probability of collecting $12 million 
●    30% probability of collecting $14 million 
●    20% probability of collecting $15 million
●    40% probability of collecting $17 million
Required: Given the estimates above, calculate the expected cash inflows for April.

Answer:

This output will be compared with estimated cash outflows for April and cash balances carried over from March to ensure that the company will have enough cash available to meet its April obligations.


Question 3: Learning Curve practice question:
The Jones Production Co. takes 50 hours to produce the first unit of its only product. 

Required: Assuming a 70 percent learning curve, estimate the average time and total time to produce two units, four units, and eight units.

Answer:

Two Units
Average time: 50 hours x 0.70 = 35 hours
Total time: 35 hours x 2 units = 70 hours 
Four Units:
Average time: 35 hours x 0.70 = 24.5 hours Total time: 24.5 hours x 4 units = 98 hours Eight Units
Average time: 24.5 hours x 0.70 = 17.15 hours
Total time: 17.15 hours x 8 units=137.2 hours

Explanation:
When the company's workers produce the first unit, it takes 50 hours. As more units are produced, workers become more efficient and produce the units at a faster pace. The learning curve is fairly steep, meaning that the biggest incremental gains in efficiency occur in the beginning; two units only take a total of 70 hours and four units take a total of 98 hours.

Because the most meaningful gains in efficiency occur early in the learning process, the curve gradually becomes less steep as production hits a steady state.