[MA/F2] Management Accounting (Kế toán Quản trị)
      Quay lại trang chủ
      1. SAPP Knowledge Base
      2. Tự học ACCA (Association of Chartered Certified Accountant)
      3. [MA/F2] Management Accounting (Kế toán Quản trị)

      [MA/F2: Tóm tắt kiến thức] Lesson 17: Các phương pháp thẩm định dự án (Method of project appraisal)

      Để ra quyết định có nên đầu tư vào một dự án hay không, doanh nghiệp cần xem xét đánh giá khả năng sinh lời và phát sinh chi phí của dự án đó, từ đó lên ngân sách chuẩn bị đầu tư và tối đa hiệu quả nguồn vốn đầu tư của mình. Ở bài này chúng ta sẽ tìm hiểu về các phương pháp (chỉ tiêu) trong thẩm định 1 dự án đầu tư của doanh nghiệp. 

      1. Thẩm định dự án (Project appraisal)

      a. Định nghĩa 

      Thẩm định dự án đầu tư là việc tổ chức xem xét đánh giá một cách khách quan, khoa học và toàn diện các nội dung cơ bản có ảnh hưởng trực tiếp đến khả năng thực hiện và hiệu quả của dự án. 

      b. Các chỉ tiêu trong thẩm định dự án

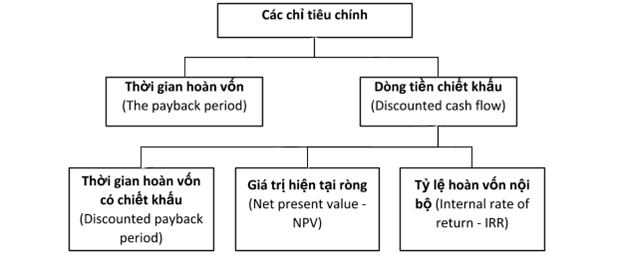
      Sau đây chúng ta sẽ cùng đi tìm hiểu thêm về từng chỉ tiêu trên.

      2. Thời gian hoàn vốn

      a. Định nghĩa 

      Thời gian hoàn vốn là khoảng thời gian cần thiết để dự án tạo ra dòng tiền thuần bằng chính số vốn đầu tư ban đầu để thực hiện dự án. 

      Lưu ý: phương pháp này sẽ ưu tiên thời gian hoàn vốn sớm hơn nếu được chọn giữa các phương án.

      Ví dụ: 

      Năm

      Machine P

      $

      Machine Q

      $

      Cost (CP vốn bỏ ra)

      		  

      10,000

      10,000

      Cash inflows year 

      (Dòng tiền vào trong năm)

      1

      1,000

      5,000
       

      2

      2,000

      5,000
       

      3

      6,000

      1,000
       

      4

      7,000

      500
       

      5

      8,000

      500

      Total (Tổng)

      		  

      24,000

      12,000

      Ta có thể thấy rằng Q có Thời gian hoàn vốn nhanh hơn – 2 năm trong khi P tới đầu năm thứ 4 mới hoàn được vốn. Vì vậy, Q sẽ được ưu tiên hơn P.

      Tuy nhiên, phương pháp này đã bỏ qua việc xem xét khả năng sinh lời của P ($24,000) gấp đôi Q ($12,000). Nên ta có thể nhận thấy rằng phương pháp này có cả ưu điểm và nhược điểm.

      b. Ưu, nhược điểm

      Ưu điểm

      Nhược điểm
      • Dễ tính toán, phân tích
      • Được sử dụng rộng rãi như một chỉ tiêu phân tích tổng quan
      • Tối thiểu hóa ảnh hưởng của tính rủi ro và tính thanh khoản
      • Giúp xác định những đối tượng có khả năng hoàn vốn nhanh
      • Bỏ qua tổng khả năng tạo ra lợi nhuận
      • Bỏ qua giá trị thời gian của dòng tiền
      • Bỏ qua những dòng tiền dự án tự bù đắp 

      Chúng ta vừa nhắc tới việc chỉ tiêu này bỏ qua giá trị thời gian của dòng tiền. Vậy chỉ tiêu thứ 2 là Dòng tiền chiết khấu có khắc phục được nhược điểm này không? Để trả lời cho câu hỏi này, trước hết, chúng ta cùng tìm hiểu xem Giá trị thời gian của dòng tiền là gì?

      3. Giá trị thời gian của dòng tiền 

      Nôm na chúng ta có thể hiểu rằng, tiền theo thời gian có thể đẻ thêm ra được tiền nếu chúng ta biết cách. Và cách phổ biến nhất đó chính là cho vay/ mang đi đầu tư và nhận lãi. Lãi thực ra chính là chi phí vay vốn (đối với người đi vay) hay giá của việc cho vay vốn (đối với người cho vay). Có rất nhiều loại lãi suất mà người ta xem xét trong việc đầu tư.

      a. Lãi kép (compound interest) 

      Lãi đơn (simple interest) là số tiền lãi được xác định chỉ dựa trên số vốn gốc (vốn đầu tư ban đầu) với một lãi suất nhất định.

      Lãi kép là số tiền lãi không chỉ tính trên số tiền gốc mà còn tính trên số tiền lãi do tiền gốc đó sinh ra. 

      Công thức tính lãi kép: 

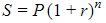
      Trong đó: 

      S – Giá trị tương lai của khoản đầu tư sau n năm/kì (tiền gốc + lãi)

      P – Giá trị hiện tại của khoản đầu tư lúc này (tiền gốc)

      r – Lãi suất của khoản đầu tư

      n – số năm/kì đầu tư

      Ví dụ luyện tập: If we invest $2,000 now at 10%, what would the investment be worth after 5 years?

      Đáp án: $3,222

      b. Chiết khấu (discounting) 

      Chiết khấu (discount) là thuật ngữ được dùng với nhiều nghĩa như:

      • Giảm giá cho một khách hàng so với bảng giá hàng hóa và dịch vụ được nhà cung cấp phát hành công khai. Chiết khấu có thể áp dụng cho việc thanh toán tiền mặt nhanh (chiết khấu tiền mặt) hoặc mua lượng hàng lớn (chiết khấu bán buôn).
      • Sự giảm giá đồng loạt của tất cả các cổ phiếu và trái phiếu khi mọi người dự kiến nền kinh tế sẽ bước vào thời kỳ suy thoái
      • Mua hối phiếu hay trái phiếu thấp hơn mệnh giá của nó.

      Chiết khấu (discounting) còn được hiểu là quá trình sử dụng lãi suất để tính giá trị hiện tại của các khoản thu hay phải trả trong tương lai. 

      Ví dụ nếu lãi suất (được dùng làm tỷ lệ chiết khấu) là 10% và khoản tiền sẽ thu được sau một năm là 110 triệu đồng, thì chúng ta có thể tính được giá trị hiện tại của khoản tiền 110 triệu đồng bằng cách lấy 110 triệu đồng chia cho (1+0,1) và được 100 triệu đồng.

      Vì vậy, ta có công thức tính chiết khấu dòng tiền ngược với công thức tính lãi kép:

      Ví dụ luyện tập: In order to build up an investment of $5,000 after 4 years at 6% interest, how much do we need to invest now?

      Đáp án: P = $5,000 x 1/ (1+0.06)^4 = 5,000 x 0.792 = $3,960

      c. Lãi suất tương đương (equivalent rate of interest)

      Lãi suất này còn có nhiều tên gọi khác như lãi suất thực hưởng (effective annual rate of interest). 

      Lãi suất thực hưởng là lãi suất thực sự kiếm được hoặc trả cho một khoản đầu tư, khoản vay hoặc sản phẩm tài chính do kết quả được tính gộp trong một khoảng thời gian nhất định. 

      Bản chất là trong thực tế nhiều trường hợp lãi suất được tính theo năm nhưng với mục tiêu thu hút khách hàng và cạnh tranh với các tổ chức tài chính khác, người ta có thể đưa ra chính sách trả lãi làm nhiều lần theo phương thức tính lãi nhập vốn nửa năm, quý, tháng… tùy theo nhu cầu của khách hàng.

      Nói cách khác, lãi suất tương đương là các lãi suất ứng với các kì tính lãi khác nhau (3 tháng, 6 tháng, 12 tháng,…) của cùng 1 khoản tiền gốc là khác nhau nhưng giá trị thu được không thay đổi. 

      Công thức tính: 

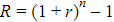
      Trong đó:

      R – lãi suất thực hưởng

      r – lãi suất tỉ lệ ứng với các kì tính lãi khác nhau

      n – số kì 

      Ví dụ: Biết lãi suất tiền gửi tiết kiệm là 12%/năm. Xác định lãi suất tỉ lệ, lãi suất tương đương của 3 tháng, 6 tháng?

      Lời giải:

      • Nếu gửi tiền kì hạn 3  tháng:

      Lãi suất tỉ lệ của ba tháng là 12%/4 = 3%

      Lãi suất tương đương của ba tháng là: (1+ 12%)^1/4 - 1 = 2.87%

      • Nếu gửi tiền kì hạn 6 tháng: 

      Lãi suất tỉ lệ của 6 tháng là 12%/2 = 6%

      Lãi suất tương đương của 6 tháng là (1+12%)^1/2 - 1 = 5.83%

      Ví dụ luyện tập: A credit card companies compounds the interest on your bill monthly. If they charge you 2% a month, does it mean they charge you 24% a year? 

      Lời giải: No, because 

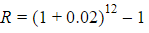
      => R = 0.2682 or 26.82% a year

      4. Dòng tiền chiết khấu (discounted cash flow)

      a. Thời gian hoàn vốn có chiết khấu

      Thời gian hoàn vốn có chiết khấu là khoảng thời gian cần thiết để tổng giá trị hiện tại tất cả dòng thu nhập trong tương lai của dự án vừa đủ bù đắp số vốn đầu tư bỏ ra ban đầu.

      Phương pháp thời gian hoàn vốn đầu tư có chiết khấu dựa vào chỉ tiêu thời gian hoàn vốn có chiết khấu để lựa chọn dự án. Theo phương pháp này thời gian hoàn vốn có chiết khấu của dự án càng ngắn thì dự án đầu tư càng hấp dẫn.

      Ví dụ: Dự án A có số vốn đầu tư là 150 triệu đồng (bỏ vốn một lần). Khoản thu nhập dự kiến (bao gồm khấu hao và lợi nhuận sau thuế) ở các năm trong tương lai như sau:

      Năm

      1

      2

      3

      4

      5

      Dự án A

      60

      50

      50

      40

      30

      Giả định chi phí sử dụng vốn của cả hai dự án là 10%. 

      Thời gian hoàn vốn có chiết khấu của dự án A như sau:

      Năm

      Dòng tiền thuần dự án (triệu đồng)

      Hệ số chiết khấu (r = 10%)

      Dòng tiền thuần đã chiết khấu (triệu đồng)

      VĐT còn phải thu hồi cuối năm (triệu đồng)

      Thời gian thu hồi lũy kế (năm)

      0

      (150)

      1

      (150)

      (150)

      		  

      1

      60

      0,909

      54,54

      (95,46)

      		  

      2

      50

      0,826

      41,13

      (54,33)

      		  

      3

      50

      0,751

      37,55

      (16,78)

      3

      4

      40

      0,683

      27,32

      		  

      16,78/27,32 = 0,61

      5

      30

      0,621

      18,63

      		    

       

      Ưu điểm

      Nhược điểm
      • Phương pháp thời gian hoàn vốn có chiết khấu đã khắc phục được hạn chế của phương pháp thời gian hoàn vốn giản đơn là xem xét dự án có tính đến giá trị thời gian của tiền.
      • Nói cách khác, phương pháp thời gian hoàn vốn có chiết khấu ghi nhận rằng chúng ta đầu tư vốn vào một dự án bất kì nào đó và sẽ kiếm lại được số tiền này bao lâu sau khi đã trừ đi chi phí cơ hội của việc sử dụng vốn.
      • Phương pháp thời gian hoàn vốn đầu tư chú trọng xem xét lợi ích ngắn hạn hơn là lợi ích dài hạn.
      • Phương pháp này ít chú trọng đến việc xem xét khoản thu sau thời gian hoàn vốn. Do đó kì hoàn vốn ngắn chưa chắc là căn cứ chính xác để lựa chọn dự án này thay vì dự án khác.
      • Đặc biệt, đối với các dự án có mức sinh lời chậm hay thời gian hoàn vốn kéo dài như dự án phát triển sản phẩm mới hay dự án xâm nhập vào thị trường mới... thì phương pháp lựa chọn dự án này sẽ không phù hợp.

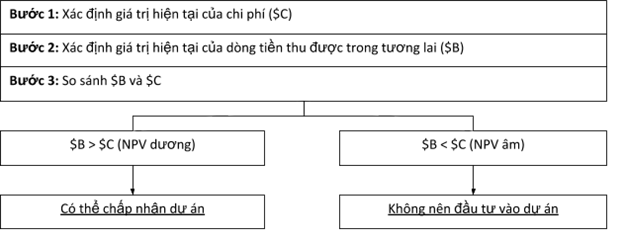
      b. Phương pháp sử dụng chỉ tiêu Net Present Value (NPV)

      Giá trị hiện tại ròng là chênh lệch giữa tổng các dòng thực thu của dự án với tổng các dòng chi phí đầu tư của dự án được quy về mặt bằng thời gian hiện tại theo một tỉ suất hoàn vốn nhất định.

      Là tổng các giá trị hiện tại của tất cả các dòng tiền của dự án.

      Ưu điểm

      Nhược điểm
      • Lợi ích của chủ sở hữu được tối đa hóa.
      • Có tính đến rủi ro và giá trị thời gian của dòng tiền. 
      • Dễ dàng trừ hoặc cộng NPV với nhau. 
      • Bộ ngân lưu tạo ra từ DA NPV có thể xem xét được. 
      • NPV phụ thuộc vào tỷ suất chiết khấu là chủ yếu để tính toán, tuy nhiên, để xác định được tỷ lệ chiết khấu lại rất khó khăn khi thị trường vốn biến động.
      • Để sử dụng được chỉ tiêu phân tích tài chính này, bạn cần nắm rõ dòng thu chi cả đời dự án. Đây là một việc mà không phải khi nào bạn cũng có thể dự kiến được.
      • Hiệu quả của một đồng vốn được sử dụng chưa được nêu rõ trong chỉ tiêu này. 
      • NPV chỉ áp dụng để tính lợi nhuận cho những dự án cùng tuổi thọ.

      Áp dụng chỉ tiêu NPV trong lựa chọn dự án đầu tư:

      c. Khoản nhận (trả) hàng năm (Annuities)

      Khoản nhận (trả) hàng năm là một loạt các khoản thanh toán được thực hiện trong khoảng thời gian bằng nhau. 

      Ví dụ về khoản nhận (trả) hàng năm: tiền gửi thường xuyên vào tài khoản tiết kiệm, thanh toán thế chấp nhà hàng tháng, thanh toán bảo hiểm hàng tháng và thanh toán lương hưu.

      Công thức:

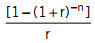
      Với r - Lãi suất tính trong kì 

            n - số lượng kì

      Ví dụ: An investor is to receive an annuity of $19,260 for 6 years commencing at the end of year 1. It has a present value of $86,400. What is the rate of interest?

      Giải: Ta có 19,260 x = 86,400. Thay n=6 => r=9%

      d. Dòng tiền đều vô hạn

      Dòng tiền đều vô hạn là khoản nhận (trả) hàng năm tồn tại mãi mãi. Giá trị hiện tại của Annuities 'a' mỗi năm, bắt đầu sau một năm, là PV = a / r trong đó r là chi phí vốn theo tỷ lệ.

      Ví dụ:

      Giá trị hiện tại của khoản nhận (trả) hàng năm $1 mỗi năm trong vô hạn, với mức chiết khấu 10% sẽ là $1 / 0.10 = $10

      Hiện nay người ta thường sử dụng thêm cả chỉ số IRR để đánh giá nguồn lợi. Do IRR dễ hình dung vì phương pháp này sử dụng theo dạng phần trăm. Chính vì thế, trong đánh giá tài chính, hai phương pháp này thường được sử dụng song song để đánh giá.

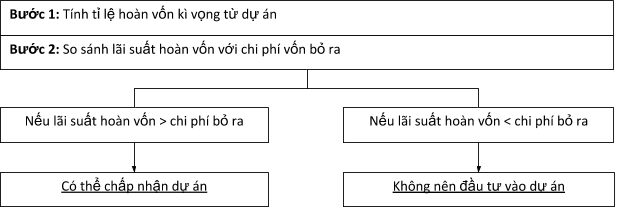
      e. Lãi suất hoàn vốn nội bộ (IRR)

      Lãi suất hoàn vốn nội bộ là lãi suất mà tại đó giá trị hiện tại của các khoản tiền thu được trong tương lai do đầu tư mang lại bằng với giá trị hiện tại của khoản vốn đầu tư hay nói cách khác tại điểm mà NPV = 0.

      Công thức tính: 

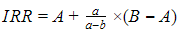
      Trong đó: 

      A – tỷ suất khấu nhỏ hơn sao cho NPV dương nhưng gần bằng 0

      B – tỷ suất khấu lớn hơn sao cho NPV âm nhưng gần bằng 0

      a – giá trị NPV tại A

      b – giá trị NPV tại B

      Áp dụng IRR trong thẩm định dự án đầu tư: 

      Ưu điểm

      Nhược điểm
      • Dễ tính toán, không bị phụ thuộc hay chi phối bởi chi phí vốn
      • Khả năng sinh lời được tính theo tỷ lệ % nên rất dễ để so sánh các dự án
      • Có thể xác định và lựa chọn lãi suất tốt nhất cho dự án đầu tư.
      • Mất nhiều thời gian để đưa ra kết quả chính xác
      • Do không sử dụng giá trị vốn để tính nên khả năng sinh lời mà IRR mang lại có thể không đúng với thực tế. Đặc biệt trong những trường hợp dự án loại bỏ nhau thì IRR còn có thể khiến các nhà đầu tư bỏ qua dự án có lãi suất ròng cao.
      • Với những dự án có đầu tư bổ sung cao, IRR sẽ rất khó xác định do NPV bị đổi dấu nhiều lần.

      Như vậy, sử dụng công thức tính IRR trong kinh doanh và đầu tư là rất cần thiết. Tuy nhiên cần phải xác định từng trường hợp và mục đích để áp dụng hiệu quả.

      5. Bài tập luyện tập

      1. A building society adds interest monthly to investors' accounts even though interest rates are expressed in annual terms. The current rate of interest is 6% per annum. An investor deposits $1,000 on 1 January. How much interest will have been earned by 30 June?

      A. $30.00

      B. $30.38

      C. $60.00

      D. $300

      Answer: B

      2. Which is worth most, at present values, assuming an annual rate of interest of 8%?

      A. $1,200 in exactly one year from now

      B. $1,400 in exactly two years from now

      C. $1,600 in exactly three years from now

      D. $1,800 in exactly four years from now 

      Answer: D

       

      Author: Ngoc Han

      Reviewed by: Duy Anh Nguyen