[PM/F5: Tóm tắt kiến thức] Lesson 11: Phân tích định lượng trong lập ngân sách (Quantitative analysis in budgeting)
Phạm vi phân tích định lượng trong lập ngân sách bao gồm 3 kỹ thuật, lần lượt là:
- High – low method
- Learning curves
- Expected values (EV)
Khả năng hiểu và áp dụng các kỹ thuật phân tích trên là một khía cạnh thiết yếu của quá trình thiết lập ngân sách nói chung và môn thi PM nói riêng. Trong bài hôm nay chúng ta sẽ tìm hiểu chi tiết.
I. Phương pháp cực đại, cực tiểu (The high - low method)
1. Định Nghĩa
High – low method là kỹ thuật phân tích tổng chi phí doanh nghiệp ở mức độ hoạt động cao nhất và thấp nhất để xác định yếu tố chi phí cố định và biến đổi.
2. Các bước thực hiện
Có 5 bước để thực hiện:
3. Ví dụ
Công ty A muốn thiết lập phương pháp dự đoán toàn bộ chi phí trong một kỳ kế toán của họ. Trong vòng 6 tháng đầu năm, họ ghi nhận các số liệu sau:
| Tháng | Mức sản xuất (chiếc) | Chi phí ($) |
| 1 | 1,600 | 28,200 |
| 2 | 2,300 | 29,600 |
| 3 | 1,900 | 28,800 |
| 4 | 1,800 | 28,600 |
| 5 | 1,500 | 28,000 |
| 6 | 1,700 | 28,400 |
Toàn bộ chi phí của công ty được thể hiện dưới dạng công thức nào?
Lời giải
- Bước 1: Xác định thời kỳ của các mức hoạt động
- Giai đoạn hoạt động lớn nhất (highest level of activity): Tháng 2 (2,300)
- Giai đoạn hoạt động thấp nhất (lowest level of activity): Tháng 5 (1,500)
- Bước 2: Điều chỉnh lạm phát
Đề bài không đề cập đến lạm phát - Bước 3: Xác định các biến số
-
- Tháng 2: sản xuất 2,300 SP và tốn $29,600
- Tháng 5: sản xuất 1,500 SP và tốn $28,000
- Bước 4: Xác định chi phí biến đổi một sản phẩm
v = (29,600 - 28,000)/(2,300 - 1,500) = 1600/800 = $2/SP
- B5: Xác định chi phí cố định
FC = 29,600 - 2 x 2,300 = $25,000
Như vậy, phương trình thể hiện toàn bộ chi phí của công ty là: 25,000 + 2x (với x là sản lượng sản xuất của một tháng)
4. Đánh giá high - low method
| Ưu điểm | Nhược điểm |
|
|
II. Đường cong học tập (Learning curve)
1. Định Nghĩa
Thuyết đường cong học tập (Learning curve theory) nghiên cứu về chi phí lao động và thời gian sản xuất khi mà lực lượng lao động được sử dụng để làm một sản phẩm mới và cải tiến hiệu quả thông qua quá trình học hỏi và tích lũy kinh nghiệm.
Thuyết này giả định là có hiện tượng học tập, đúc rút kinh nghiệm sau mỗi sản phẩm sản xuất giúp năng suất sản phẩm được nâng cao.
Từ đó, có 2 khái niệm xuất hiện:
- Tỷ lệ học tập (Learning rate): được thể hiện dưới dạng phần trăm (VD: 90%,80%)
- Hiệu quả học tập(Learning effect): là ảnh hưởng của quá trình tiếp thu kinh nghiệm làm việc đến năng suất lao động.
Do đó, mỗi khi năng suất tăng gấp đôi, thì thời gian sản xuất trung bình từng sản phẩm sẽ giảm theo tỉ lệ learning rate.
2. Điều kiện áp dụng
Thuyết này được áp dụng khi sản phẩm thỏa mãn bất kỳ điều kiện nào sau đây:
- Được sản xuất bằng năng lực lao động là chính thay vì dựa vào máy móc, thiết bị
- Là sản phẩm mới (quá trình học tập không kéo dài vô thời hạn);
- Sản phẩm phức tạp, sản xuất số lượng nhỏ cho các đơn hàng đặc biệt.
3. Ví dụ
Learning rate là 80%, thời gian sản xuất sản phẩm đầu là 100 (tiếng). Mỗi khi số lượng sản phẩm tăng gấp đôi, thời gian trung bình sản xuất các sản phẩm sẽ giảm còn 80%.
Với 2 sản phẩm, thời gian trung bình sản xuất là 100 x 80% = 80 (tiếng)
Với 4 sản phẩm, thời gian trung bình sản xuất là 80 x 80% = 64 (tiếng)
| Số lượng | Thời gian trung bình | Tổng thời gian | Thời gian tăng thêm |
| 1 | 100 | (100 x 1) = 100 | 100 |
| 2 | (100 x 80%) = 80 | (80 x 2) = 160 | (160 – 100) = 60 |
| 4 | (80 x 80%) = 64 | (64 x 4) = 256 | (256 – 160) = 96 |
4. Các dạng thể hiện
Đường cong học tập có 2 dạng thể hiện sau:
(a) Dạng đại số (Algebraic Approach)
Công thức cho learning curve là: 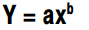
Trong đó:
- Y: thời gian trung bình tích lũy (hoặc chi phí trung bình) trên mỗi đơn vị sản phẩm để sản xuất x sản phẩm
- x: số sản phẩm tích lũy
- a: thời gian sản xuất sản phẩm đầu tiên
- b: chỉ số học tập (=logr/log2)
- r: tỉ lệ học tập, thể hiện dưới dạng thập phân
Chú ý: Công thức sẽ được cung cấp trong đề thi, không cần học thuộc
Ví dụ:
Sản phẩm ABC có learning curve là 80%. Doanh nghiệp hiện tại đã sản xuất xong 30 chiếc ABC. Chiếc ABC đầu tiên sản xuất mất 120 tiếng làm việc. Hỏi thời gian cần thiết để sản xuất chiếc ABC số 31 là bao nhiêu tiếng?
Lời giải
Thời giản sản xuất chiếc ABC số 31 sẽ bằng tổng thời gian sản xuất 31 chiếc trừ đi tổng thời gian sản xuất 30 chiếc.
Để giải bài toán ta cần tìm hết các biến số cần thiết cho công thức Y = ax^b
- b = log 0.8/log 2 = (0.3219281)
- x = 30
- a = 120
Thời gian trung bình để sản xuất mỗi sản phẩm khi sản xuất 30 chiếc:
Y(30) = 30^(-0.3219281) x 120 = 40.147 (tiếng/chiếc)
Tổng thời gian sản xuất 30 chiếc
40.147 x 30 = 1,204.41 (tiếng)
Thời gian trung bình để sản xuất mỗi sản phẩm khi sản xuất 31 chiếc:
Y(31) = 31^(-0.3219281) x 120 = 39.726 (tiếng/chiếc)
Tổng thời gian sản xuất 31 chiếc
39.726 x 31 = 1,231.51 (tiếng)
Thời gian sản xuất chiếc ABC số 31 là: 1,231.51 – 1,204.41 = 27.1 (tiếng)
(b) Dạng biểu (Tabular Approach)
Dạng biểu chỉ được sử dụng trong trường hợp tính thời gian trung bình khi sản phẩm tích lũy tăng gấp đôi. Bởi vậy, dạng biểu được đánh giá là dễ hơn nhưng dạng đại số có khả năng cao hơn gặp trong bài thi môn này.
Ví dụ:
Learning curve của một doanh nghiệp là 90%, tức thời gian trung bình tổng bình sản xuất 1 sản phẩm giảm còn 90% mỗi khi sản lượng sản xuất tăng gấp đôi, ta có thể lập bảng sau:
| Tổng sản phẩm | Thời gian sản xuất trung bình mỗi sản phẩm | Tổng thời gian | Số sản phẩm tăng thêm | Số thời gian tăng thêm |
| 1 | 100 | 100 | - | - |
| 2* | 90 | 180 | 1 | 80 |
| 4* | 81 | 324 | 2 | 144 |
| 8* | 73 | 583 | 4 | 259 |
| 16* | 66 | 1050 | 8 | 467 |
(*) Lượng sản phẩm đầu ra tăng gấp đôi mỗi lần.
5. Đánh giá Learning curve
| Ưu điểm | Nhược điểm |
|
|
III. Giá trị kỳ vọng (Expected value - EV)
1. Định Nghĩa
Giá trị kỳ vọng (EV) là kỹ thuật sử dụng trong quá trình lập ngân sách nhằm xác định kết quả tốt nhất giữa lợi nhuận kỳ vọng và khả năng xảy ra.
Ngân sách xác suất (probabilistic budgeting) xác định xác suất cho từng kết quả có thể diễn ra (khả thi nhất, bất lợi nhất, khả thi nhất…) để tổng hợp thành giá trị EV của lợi nhuận ngân sách.
Ví dụ:
Một công ty đang đánh giá khả năng lãi của việc áp dụng một ngân sách đang được đề xuất và có các ước tính sau:
| Profit/(loss) | Probability | |
| $’000 | % | |
| Worst outcome | (220) | 30% |
| Likely outcome | 300 | 60% |
| Best outcome | 770 | 10% |
Giá trị kỳ vọng sẽ được tính như sau:
| Profit/(loss) | Probability | EV | |
| (a) | (b) | (a*b) | |
| Worst outcome | (220) | 30% | (66) |
| Likely outcome | 300 | 60% | 180 |
| Best outcome | 770 | 10% | 77 |
| EV profit | 191 |
2. Đánh giá EV
Mặc dù, kỹ thuật này được xem là khá đơn giản để sử dụng trong phân tích định lượng ngân sách, nhưng EV vẫn tồn tại những hạn chế sau:
- Việc chuẩn bị ngân sách xác suất tốn nhiều thời gian hơn ngân sách cố định thông thường, chi phí có thể vượt quá lợi ích mang lại
- EV thể hiện giá trị trung bình theo xác suất và giá trị này có thể không tồn tại trong thực tế Cụ thể, ở ví dụ trên, thực tế doanh nghiệp có thể sẽ lãi $300,000, $700,000 hoặc lỗ $220,000. Giá trị thực tế sẽ không bao giờ là $191,000.
Author: QM