[Quantitative concepts] Thống kê mô tả

Tóm tắt các kiến thức quan trọng về Thống kê mô tả trong môn Quantitative concepts thuộc chương trình CFA Institute Investment Foundation.

Nếu bạn cần thêm thông tin, đừng quên liên hệ với chúng tôi:

I. Tổng quan

• Những kiến thức cần nhớ về thống kê mô tả
• Tần suất và trung bình
• Độ phân tán
• Hiệp phương sai
• Hệ số tương quan

Xem thêm slides môn học tại đây

II. Nội dung

1. Những kiến thức cần nhớ về xác suất và thống kê

a. Xác suất

- Mô tả khả năng một sự kiện có thể xảy ra.

- Xác suất của một sự kiện nằm trong khoảng từ 0 đến 1 (0% - 100%)

b. Các quy tắc 

Quy tắc cộng:

+ A và B xung khắc: Nếu A xảy ra thì B không thể xảy ra.

→ Xác suất để A hoặc B xảy ra được tính bởi công thức:

P(A or B) = P(A) + P(B)

+ A và B không xung khắc: A và B có thể đồng thời xảy ra.

→ Xác suất để A hoặc B xảy ra được tính bởi công thức:

P(A or B) = P(A) + P(B) – P(A&B)

Quy tắc nhân:

+ A và B độc lập: Xác suất xảy ra của A không ảnh hưởng đến B

→ Xác suất xảy ra của A và B được tính bởi công thức:

P(A & B) = P(A) x P(B)

+ A và B phụ thuộc: Kết quả xảy ra của A ảnh hưởng đến B

→ Xác suất xảy ra của A và B được tính bởi công thức:

P(A&B) = P(B) x P(A|B)

c. Các công thức cần nhớ

	Hoán vị	Chỉnh hợp	Tổ hợp
Định nghĩa	Cho tập hợp A, gồm n phần tử (n>=1). Một cách sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử đó.	Cho tập hợp A gồm n phần tử. Một bộ gồm k (1 <= k <= n) phần tử sắp xếp thứ tự của tập hợp A được gọi là một chỉnh hợp chập k của n phần tử của tập hợp A.	Cho tập hợp A gồm n phần tử. Một tập con của A, gồm k phần tử phân biệt (1 <= k <= n), được gọi là một tổ hợp chập k của n phần tử của A.
Công thức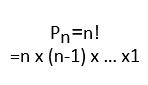

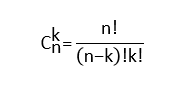2. Tần suất và trung bình

a. Trung bình cộng

Là giá trị của toàn bộ các quan sát trong tập chia cho số lượng các quan sát trong tập.

b. Trung bình nhân

Là chỉ số thường được sử dụng nhất để tính tốc độ thay đổi trung bình theo thời gian hoặc để tính tốc độ tăng trưởng của một biến.

Công thức: 

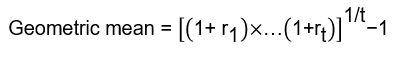
c. Trung vị (median)

Là điểm giữa của tập dữ liệu khi dữ liệu được sắp xếp theo thứ tự tăng dần hoặc giảm dần. Một nửa số quan sát nằm trên giá trị trung vị và một nửa còn lại nằm dưới giá trị trung vị. 

d. Yếu vị (mode)

- Là giá trị xuất hiện thường xuyên nhất trong tập dữ liệu.

+ Unimodal: Khi phân phối chỉ có một giá trị xuất hiện thường xuyên nhất .

+ Bimodal or trimodal: Khi phân phối có 2 hoặc 3 giá trị xuất hiện thường xuyên nhất.

e. Khoảng biến thiên

Là khoảng cách giữa giá trị lớn nhất và giá nhỏ nhất của một tập hợp.

Công thức: 

Khoảng biến thiên = Giá trị lớn nhất - Giá trị nhỏ nhất

3. Độ phân tán

a. Độ lệch chuẩn

Là một đại lượng thống kê mô tả dùng để đo mức độ phân tán của một tập dữ liệu xung quanh giá trị trung bình (mean) của tập dữ liệu đó.

Công thức: 

b. Phân phối chuẩn

Khái niệm: Là sự phân bố dữ liệu mà ở đó giá trị tập trung nhiều nhất ở khoảng giữa và càng về hai bên thì xác suất của các giá trị càng giảm dần (xem hình minh họa).

Đặc điểm:

+ Được biểu diễn bởi biều đồ cong hình chuông.

+ Có tầm quan trọng đặc biệt trong thống kê vì nhiều phân bố xác suất có hình dạng tương tự như vậy.

4. Hiệp phương sai (Covariance) 

Khái niệm: là đại lượng phản ánh mức độ tương quan tuyến tính của hai biến số.

+ Hiệp phương sai dương: Hai biến chuyển động cùng chiều.

+ Hiệp phương sai âm: Hai biến chuyển động ngược chiều.

Công thức: 

5. Hệ số tương quan (Correlation):

Khái niệm: Là chỉ số thống kê đo lường mức độ mạnh yếu của mối quan hệ tương quan giữa hai biến số.

Đặc điểm: Hệ số tương quan có giá trị từ -1.0 đến 1.0. Kết quả được tính ra lớn hơn 1.0 hoặc nhỏ hơn -1 có nghĩa là có lỗi trong phép đo tương quan.

+ Hệ số tương quan có giá trị âm cho thấy hai biến có mối quan hệ nghịch biến hoặc tương quan âm (nghịch biến tuyệt đối khi giá trị bằng -1)

+ Hệ số tương quan có giá trị dương cho thấy mối quan hệ đồng biến hoặc tương quan dương (đồng biến tuyệt đối khi giá trị bằng 1)

+ Tương quan bằng 0 cho hai biến độc lập với nhau.

Công thức:

Reviewer: Hoang Ngoc

SAPP Academy