[Tóm tắt kiến thức quan trọng] Module 6: Simulation Methods
Bài viết cung cấp cho người đọc kiến thức về Module 6 môn Quantitative Methods của chương trình CFA level I
[LOS 6.a] Giải thích mối quan hệ giữa phân phối chuẩn và phân phối loga chuẩn; trình bày lý do phân phối loga chuẩn được sử dụng để lập mô hình định giá tài sản
Phân phối loga chuẩn được tạo ra bởi hàm,![]() . Trong đó, x được phân phối chuẩn. Phân phối loga chuẩn có các đặc tính chính như sau:
. Trong đó, x được phân phối chuẩn. Phân phối loga chuẩn có các đặc tính chính như sau:
-
Phân phối loga chuẩn bị lệch sang phải, do giới hạn dưới luôn là 0.
-
Phân phối loga chuẩn không bao giờ âm.
Công thức của continuous compounding
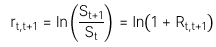
[Pre.i] Mô tả các tính chất của phân phối Student's T; tính toán và giải thích các bậc tự do của nó
Phân phối T: Phân phối T là phân phối xác suất đối xứng được xác định bởi một tham số duy nhất được gọi là bậc tự do (degree of freedom).
Phân phối T so với phân phối chuẩn:
-
Phân phối T có đuôi béo hơn so với phân phối chuẩn.
-
Bậc tự do (degree of freedom): df = n-1 (n là cỡ mẫu).
-
Khi df tăng, hình dạng của phân phối t tiến tới phân phối chuẩn.
[Pre.ii] Mô tả các tính chất của phân phối Chi-square và phân phối F; tính toán và giải thích các bậc tự do của chúng
Phân phối Chi-square: Phân phối Chi-square là tổng bình phương của k biến ngẫu nhiên chuẩn độc lập có phân phối chuẩn. Phân phối Chi-square có các đặc tính chính sau:
-
Hình dạng của nó là không đối xứng.
-
Nó không nhận các giá trị âm.
Phân phối F: Phân phối F là phân phối không đối xứng được giới hạn từ bên dưới bởi 0 và liên quan trực tiếp đến phân phối Chi-square.
-
Phân phối F có 2 bậc tự do.
-
Khi bậc tự do của cả tử số (df1) và mẫu số (df2) đều tăng, hàm mật độ cũng sẽ trở thành đường cong giống hình chuông hơn.
[LOS 6.c] Mô tả các phương pháp tái chọn mẫu để ước tính phân phối lấy mẫu của một thống kê
Tái chọn mẫu (resampling) là một công cụ tính toán lặp lại các mẫu từ mẫu dữ liệu quan sát ban đầu để suy luận thống kê các tham số dân số.
Các phương pháp lấy mẫu phổ biến:
-
Bootstrap: Lấy mẫu bằng cách lặp đi lặp lại từ mẫu ban đầu để tìm sai số chuẩn và khoảng tin cậy.
-
Jackknife: Lấy mẫu dữ liệu quan sát ban đầu và loại bỏ một quan sát tại một thời điểm từ tập hợp (và không thay thế nó).