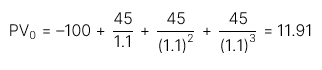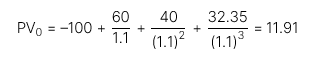[Tóm tắt kiến thức quan trọng] Module 2: The Time Value of Money
Bài viết cung cấp cho người đọc kiến thức về Module 2 môn Quantitative Methods của chương trình CFA level I
[Pre.i] Tính toán giá trị tương lai (FV) và giá trị hiện tại (PV) của từng kiểu dòng tiền khác nhau
1. Giá trị tương lai (Future value)
Là giá trị có thể nhận được tại một thời điểm trong tương lai bao gồm số vốn gốc và tiền lãi phát sinh.
1.1. Giá trị tương lai của dòng tiền đơn (Future value of a lump sum)
Ghép lãi hàng năm (Annually compounding):
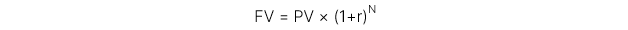
Ghép lãi hàng kỳ (Periodically compounding):
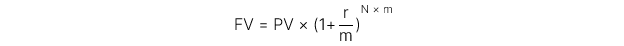
Ghép lãi liên tục (Continuously compounding):
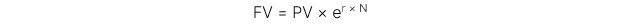
Trong đó:
-
r = Lãi suất công bố hàng năm
-
m = Số lần ghép lãi trong một năm
-
N = Số năm
Lưu ý: Số lần ghép lãi trong 1 năm (m) càng lớn thì future value (FV) càng lớn.
1.2. Giá trị tương lai của chuỗi dòng tiền đều (Future value of annuity)
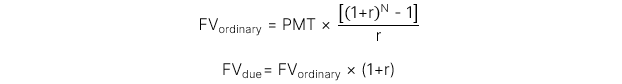
2. Giá trị hiện tại (Present value)
Là giá trị của khoản tiền phát sinh trong tương lai được chiết khấu về thời điểm hiện tại.
2.1. Giá trị hiện tại của chuỗi dòng tiền đơn (Present value of a lump sum)
Ghép lãi hàng năm (Annually compounding):
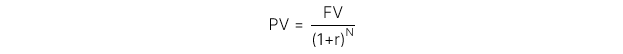
Ghép lãi hàng kỳ (Periodically compounding):
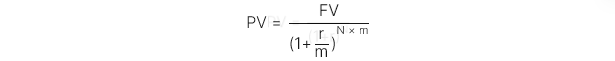
Ghép lãi liên tục (Continuously compounding):
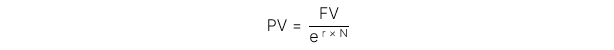
2.2. Giá trị hiện tại của chuỗi dòng tiền đều (Present value of annuity)
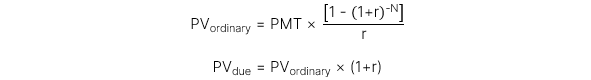
2.3. Giá trị hiện tại của dòng tiền đều vô hạn (Present value of a perpetuity)
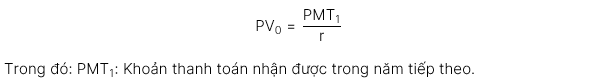
3. Cách tính dòng tiền không đồng đều: Tính toán giá trị hiện tại (PV) hoặc giá trị tương lai (FV) của các dòng tiền không đồng đều có thể được thực hiện bằng cách tổng hợp PV hoặc FV của mỗi dòng tiền riêng lẻ:
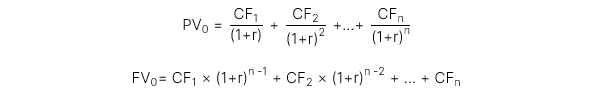
[LOS 2.a] Tính toán giá trị hiện tại (PV) và lợi nhuận (r) của chứng khoán thu nhập cố định
Chứng khoán thu nhập cố định, ví dụ như trái phiếu hoặc khoản cho vay, là một công cụ tài chính cho phép tổ chức phát hành chứng khoán nợ để vay mượn của nhà đầu tư. Tổ chức đó có nghĩa vụ pháp lý phải trả gốc lẫn lãi nhà đầu tư trong khoảng kỳ hạn nhất định.
Phần lớn chứng khoán nợ được phát hành dưới dạng trái phiếu (bond) xác nhận bên A mang nợ bên B một khoản tiền. Bên phát hành A (issuers) có nghĩa vụ trả gốc và lãi cho bên mua trái phiếu B (bond holder) trong kỳ hạn nhất định.
Dòng tiền từ chứng khoán nợ thường được mô tả dưới 3 dạng công cụ:
-
Discount instruments
-
Coupon instruments
-
Annuity instruments
1. Discount instruments
a. Đặc điểm:
Nhà đầu tư không nhận được lãi suất hàng kỳ mà thay vào đó, nhà đầu tư trả giá ban đầu (PV) cho một trái phiếu hoặc khoản vay và nhận được một dòng tiền gốc (FV) duy nhất vào ngày đáo hạn. Chênh lệch (FV - PV) thể hiện cho tiền lãi thu được trong suốt thời gian sử dụng của công cụ.
b. Công thức tính giá trị hiện tại (PV):
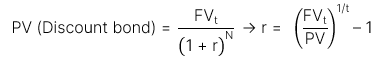
2. Coupon instruments
a. Đặc điểm:
Nhà đầu tư trả giá ban đầu (PV) cho trái phiếu hoặc khoản vay và nhận dòng tiền lãi (PMT) theo các khoảng thời gian xác định trước (định kỳ) trong thời hạn của trái phiếu, với khoản thanh toán lãi cuối cùng và số tiền gốc (FV) được trả vào ngày đáo hạn.
b. Công thức tính giá trị hiện tại (PV):
-
Trái phiếu có kỳ hạn xác định:
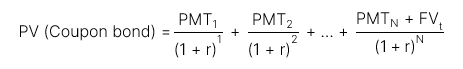
-
Trái phiếu có kỳ hạn vĩnh cửu, không có FV:
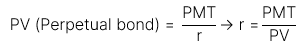
3. Annuity instruments
a. Đặc điểm:
Nhà đầu tư trả giá ban đầu (PV) cho trái phiếu hoặc khoản vay và nhận dòng tiền (PMT) bao gồm tiền lãi và một phần tiền gốc hàng kỳ trong trong thời hạn của trái phiếu. Cho đến khi trái phiếu đáo hạn, số tiền gốc đã được trả hết và phân bổ trong thời hạn của trái phiếu.
b. Công thức tính giá trị hiện tại (PV):
-
Dòng tiền niên kim cuối kỳ (ordinary annuity):
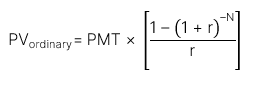
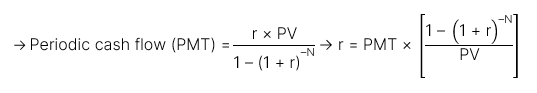
[LOS 2.b] Tính toán giá trị hiện tại (PV) của chứng khoán vốn
Chứng khoán vốn, chẳng hạn như cổ phiếu ưu đãi hoặc cổ phiếu phổ thông, đại diện cho quyền sở hữu trong một công ty cổ phần, cho phép các nhà đầu tư nhận các dòng tiền dưới dạng cổ tức.
Không giống như các chứng khoán thu nhập cố định, chứng khoán vốn không có ngày đáo hạn và được giả định là tồn tại vô thời hạn hoặc cho đến khi công ty được bán, cơ cấu lại hoặc thanh lý.
Dòng tiền từ chứng khoán vốn thường được mô tả dưới 3 dạng:
-
Cổ tức cố định
-
Cổ tức có tốc độ tăng trưởng cố định
-
Cổ tức có tốc độ tăng trưởng thay đổi
1. Cổ tức cố định
a. Đặc điểm:
Nhà đầu tư trả giá ban đầu (PV) cho cổ phiếu ưu đãi hoặc cổ phiếu phổ thông và nhận được cổ tức cố định hàng kỳ (D).
b. Công thức:
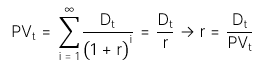
2. Cổ tức có tốc độ tăng trưởng cố định
a. Đặc điểm:
Nhà đầu tư trả giá ban đầu (PV) cho một cổ phiếu và nhận được cổ tức ban đầu trong một kỳ 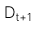 , dự kiến sẽ tăng theo thời gian với tốc độ không đổi là g.
, dự kiến sẽ tăng theo thời gian với tốc độ không đổi là g.
b. Công thức tính PV:
Cổ tức vào kỳ i là:
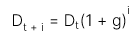
Giá trị ban đầu PV của cổ phiếu khi cổ tức tăng trưởng với tốc độ không đổi g (r > g) trong khoảng thời gian vô hạn là:
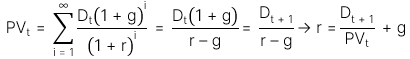
3. Cổ tức có tốc độ tăng trưởng thay đổi
a. Đặc điểm:
Nhà đầu tư trả giá ban đầu (PV) cho một cổ phiếu và nhận được cổ tức ban đầu trong một kỳ 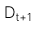 . Cổ tức dự kiến sẽ tăng với tốc độ thay đổi theo thời gian khi công ty chuyển từ giai đoạn đầu của tăng trưởng cao sang tăng trưởng chậm hơn khi công ty đạt đến giai đoạn trưởng thành. Một công ty có tốc độ tăng trưởng quá cao sẽ không thể duy trì đà phát triển này vô thời hạn do nó sẽ thu hút sự cạnh tranh. Vì vậy tốc độ tăng trưởng của doanh nghiệp đó cuối cùng sẽ giảm xuống.
. Cổ tức dự kiến sẽ tăng với tốc độ thay đổi theo thời gian khi công ty chuyển từ giai đoạn đầu của tăng trưởng cao sang tăng trưởng chậm hơn khi công ty đạt đến giai đoạn trưởng thành. Một công ty có tốc độ tăng trưởng quá cao sẽ không thể duy trì đà phát triển này vô thời hạn do nó sẽ thu hút sự cạnh tranh. Vì vậy tốc độ tăng trưởng của doanh nghiệp đó cuối cùng sẽ giảm xuống.
b. Công thức tính PV:
Giai đoạn tăng trưởng ban đầu với tốc độ tăng trưởng là 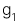 trong n thời kỳ, sau đó là giai đoạn tăng trưởng với tốc độ tăng trưởng là
trong n thời kỳ, sau đó là giai đoạn tăng trưởng với tốc độ tăng trưởng là 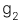 trong khoảng thời gian vô hạn:
trong khoảng thời gian vô hạn:
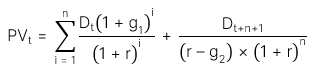
Ngoài ra, thay vì so sánh giá cổ phiếu trực tiếp bằng tiền tệ, một cách phổ biến là so sánh chỉ số giá cổ phiếu với thu nhập trên mỗi cổ phiếu hoặc chỉ số giá trên thu nhập.
Công thức tính PV khi tốc độ tăng trưởng không đổi:
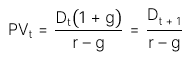
Trường hợp 1: Chia cả hai vế của công thức trên cho 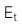 là thu nhập trên mỗi cổ phiếu của kỳ t, ta có:
là thu nhập trên mỗi cổ phiếu của kỳ t, ta có:
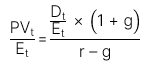
Trường hợp 2: Chia cả hai vế của công thức trên cho 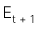 là thu nhập trên mỗi cổ phiếu của kỳ tiếp theo (t + 1), ta có:
là thu nhập trên mỗi cổ phiếu của kỳ tiếp theo (t + 1), ta có:
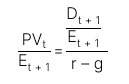
Chỉ số cổ tức/EPS, hay còn được gọi là tỷ lệ chi trả cổ tức, là tỷ lệ lợi nhuận được chia cho cổ đông dưới dạng cổ tức.
[LOS 2.c] Tính toán lãi suất hàng năm và lãi suất ghép lãi liên tục và các trường hợp áp dụng các lãi suất này
1. Lãi suất hàng năm
Khi kỳ ghép lãi không phải hàng năm nhưng lợi nhuận thu được trong khoảng thời gian ngắn hơn (hoặc dài hơn) hơn một năm, chúng ta sẽ phải tính lợi nhuận hàng năm cho khoảng thời gian này.
Giả định: Lợi nhuận có thể được lặp lại một cách chính xác → tiền có thể được tái đầu tư nhiều lần trong khi vẫn kiếm được lợi nhuận tương tự.
Ta có công thức tính lãi suất hàng năm như sau:
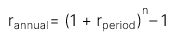
Trong đó:
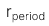 là lãi suất kiếm được trong một kỳ.
là lãi suất kiếm được trong một kỳ.
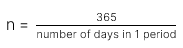 : là số kỳ trong một năm.
: là số kỳ trong một năm.
2. Lãi suất ghép lãi liên tục
Holding period return (HPR) còn gọi là lợi tức nắm giữ định kỳ, là tổng lợi nhuận thu được khi nắm giữ một tài sản hay danh mục tài sản trong một khoảng thời gian nhất định.
Giả sử giá của cổ phiếu trong một giai đoạn tăng từ 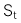 đến
đến 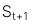 , ta có công thức tính HPR như sau:
, ta có công thức tính HPR như sau:
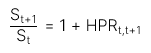
Giả sử rằng giá của tài sản 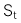 được ghép lãi đến
được ghép lãi đến 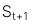 với lãi suất ghép lãi liên tục là
với lãi suất ghép lãi liên tục là 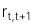 , ta có công thức như sau:
, ta có công thức như sau:
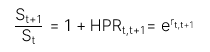
Để xác định lãi suất 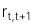 , ta thêm logs vào hai vế của công thức trên, ta có:
, ta thêm logs vào hai vế của công thức trên, ta có:
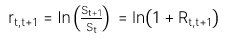
[Pre.ii] Diễn giải vai trò của dòng thời gian trong việc lập mô hình và giải quyết các vấn đề liên quan tới giá trị thời gian của dòng tiền
Nguyên tắc cộng các dòng tiền (Cash flow additivity rule)
Nguyên tắc chính

Cách sử dụng
Nguyên tắc có thể được sử dụng để giải quyết các vấn đề với dòng tiền không đồng đều bằng cách kết hợp các khoản thanh toán và niên kim đơn lẻ.
[LOS 2.d] Giải thích quy tắc cộng của dòng tiền, tầm quan trọng của nó đối với điều kiện không tồn tại kinh doanh chênh lệch giá và ứng dụng trong tính toán lãi suất kỳ hạn, tỷ giá hối đoái kỳ hạn và giá trị của quyền chọn
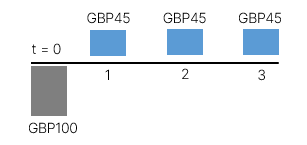
Giả sử rằng bạn có GBP100 để đầu tư và có hai chiến lược để lựa chọn với các dòng tiền như minh họa bên dưới. Lợi tức yêu cầu của bạn cho cả hai chiến lược đầu tư là 10% trong khoảng thời gian đầu tư.
Cách 1: Tính PV của từng dòng tiền
|
|
Timeline của dòng tiền |
Giá trị hiện tại của dòng tiền |
|
Dòng tiền 1 |
|
|
|
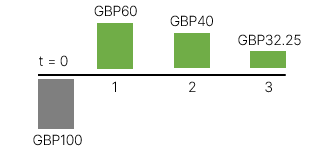
Dòng tiền 2 |
|
|
→ Vì giá trị hiện tại của hai dòng tiền là bằng nhau nên ta có thể sử dụng một trong hai chiến lược trên.
Cách 2: Tạo ra dòng tiền là chênh lệch giữa hai dòng tiền của hai chiến lược trên
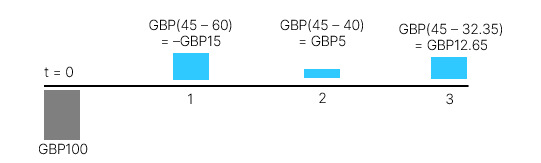
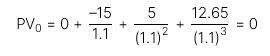
→ Giá trị hiện tại của các dòng tiền chênh lệch này bằng 0 → hai chiến lược có giá trị về mặt kinh tế tương đương nhau, do đó ta không nên ưu tiên cái này hơn cái kia.
Ứng dụng: Tính giá trị hiện tại và giá trị tương lai của chuỗi dòng tiền không đều. Theo quy tắc cộng dòng tiền, các dòng tiền phát sinh tại cùng thời điểm có thể cộng gộp mà không làm thay đổi tổng giá trị của chuỗi dòng tiền. Do đó tổng giá trị của A và B bằng A + B. Ngược lại, chuỗi dòng tiền A + B có thể tách thành hai chuỗi dòng tiền A và B mà không làm thay đổi tổng giá trị của chuỗi.
1. Tính lãi suất kỳ hạn sử dụng quy tắc cộng dòng tiền
Minh họa: Hai trái phiếu chiết khấu phi rủi ro với kỳ hạn khác nhau có lãi suất như sau:
Trái phiếu kỳ hạn 1 năm: 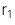 = 2.50%
= 2.50%
Trái phiếu kỳ hạn 2 năm: 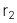 = 3.50%
= 3.50%
Một nhà đầu tư muốn kiếm lợi nhuận là GBP100 trong thời gian đầu tư hai năm có hai chiến lược như sau:
Chiến lược 1: Đầu tư ngay hôm nay với kỳ hạn 2 năm tại lãi suất tương ứng với kỳ hạn là 3.5%.
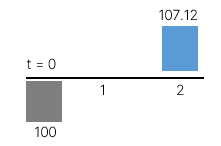
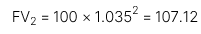
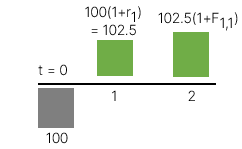
Theo nguyên tắc cộng dòng tiền, nhà đầu tư sẽ không quan tâm đến chiến lược 1 và 2 với điều kiện sau.
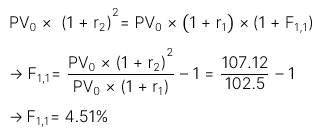
2. Tính tỷ giá hối đoái kỳ hạn bằng cách sử dụng quy tắc cộng dòng tiền
Tỷ giá hối đoái kỳ hạn được tính toán theo nguyên tắc đảm bảo rằng các nhà giao dịch không thể kiếm được kinh doanh chênh lệch giá. Điều này có nghĩa là nhà giao dịch đầu tư theo đồng tiền nội tệ hay đầu tư bằng bất kỳ loại tiền tệ nào khác đều sẽ kiếm được số tiền tương tự.
Chiến lược đầu tư tổng quan như sau:
-
Lựa chọn 1: Đầu tư trực tiếp bằng đồng tiền nội tệ
-
Lựa chọn 2: Ban đầu đầu tư vào đồng tiền ngoại tệ, sau đó nhận được lợi nhuận từ việc đầu tư và chuyển đối các khoản tiền này về đồng ngoại tệ.
Để loại bỏ cơ hội kinh doanh chênh lệch giá thì thu nhập ở cả 2 lựa chọn này phải bằng nhau.
(Đọc thêm ở môn Economics, Module 8)
3. Tính giá trị của quyền chọn bằng cách sử dụng quy tắc cộng dòng tiền
Quyền chọn là một hợp đồng phái sinh, trong đó một bên (người mua) sẽ phải trả một khoản tiền (phí bảo hiểm) cho bên kia (người bán) và nhận quyền mua hoặc bán một tài sản cơ bản tại một mức giá cố định vào ngày đáo hạn hoặc vào bất kỳ thời điểm nào trước ngày đáo hạn tùy theo thỏa thuận.
Có hai loại quyền chọn:
-
Quyền chọn mua (call option): Người mua có quyền mua tài sản cơ bản tại một mức giá xác định trong khoảng thời gian theo thỏa thuận.
-
Quyền chọn bán (put option): Người mua có quyền bán tài sản cơ bản tại một mức giá xác định trong khoảng thời gian theo thỏa thuận.
Đánh giá giá trị quyền chọn bằng tỷ lệ phòng hộ hedge ratio:
Tỷ lệ phòng hộ rủi ro là tỷ lệ tài sản cơ sở sẽ bù đắp cho rủi ro liên quan đến quyền chọn (tức là số lượng cổ phiếu của tài sản cơ sở mà chúng ta sẽ mua cho mỗi quyền chọn mua mà chúng ta sẽ bán).
Chiến lược đầu tư tổng quan
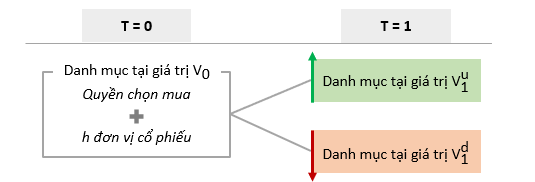
Để loại bỏ cơ hội kinh doanh chênh lệch giá thì giá trị ở cả 2 biến động giá phải giống nhau.
(Đọc thêm ở môn Derivatives, Module 11)