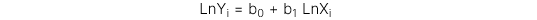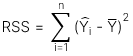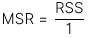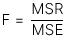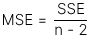[Tóm tắt kiến thức quan trọng] Module 10: Simple Linear Regression
Bài viết cung cấp cho người đọc kiến thức về Module 10 môn Quantitative Methods của chương trình CFA level I
[LOS 10.a] Mô tả mô hình hồi quy tuyến tính đơn và Mô tả tiêu chí bình phương tối thiểu và cách sử dụng để ước tính các hệ số hồi quy
1. Mục đích của hồi quy tuyến tính đơn biến (simple linear regression)
Hồi quy tuyến tính đơn biến được sử dụng để giải thích sự thay đổi của biến phụ thuộc dựa trên sự thay đổi của một biến độc lập duy nhất.
2. Mô hình hồi quy tuyến tính đơn biến (simple linear regression model)
Mô hình hồi quy này được công thức hóa như sau:
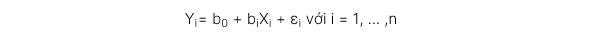
Trong đó:
-
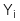 : Quan sát thứ i của biến phụ thuộc Y
: Quan sát thứ i của biến phụ thuộc Y -
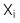 : Quan sát thứ i của biến phụ thuộc X
: Quan sát thứ i của biến phụ thuộc X -
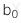 : Hệ số chặn (Intercept)
: Hệ số chặn (Intercept) -
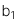 : Hệ số góc (Slope coeficient hay Regression coeficient)
: Hệ số góc (Slope coeficient hay Regression coeficient) -
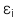 : Phần dư (Residual hay Error term) chính là chênh lệch giữa giá trị thực tế và giá trị được dự đoán bởi phương trình hồi quy của quan sát thứ i,
: Phần dư (Residual hay Error term) chính là chênh lệch giữa giá trị thực tế và giá trị được dự đoán bởi phương trình hồi quy của quan sát thứ i,  .
.
2.1. Biến phụ thuộc (dependent variable)
Biến phụ thuộc là biến số chịu ảnh hưởng của một biến số khác trong mô hình hồi quy. Sự thay đổi của biến phụ thuộc được giải thích bởi biến độc lập.
Biến phụ thuộc còn có các tên gọi khác như explained variable, endogenous variable, predicted variable.
2.2. Biến độc lập (independent variable)
Biến độc lập (independent variable) là biến số tác động tới biến số khác (biến phụ thuộc) trong mô hình hồi quy. Biến độc lập được sử dụng để giải thích cho sự thay đổi của biến phụ thuộc
Biến độc lập còn có các tên gọi khác như explanatory variable, exogenous variable, predicting variable.
3. Tiêu chí bình phương tối thiểu và cách sử dụng để ước tính các hệ số hồi quy
3.1. Đường hồi quy (regression line)
3.1.1. Định nghĩa
Đường hồi quy là đường tối thiểu hóa tổng sai số bình phương (SSE - sum of the squares error) giữa các giá trị Y được dự đoán bởi phương trình hồi quy và các giá trị Y thực tế.
Đây là lý do vì sao hồi quy tuyến tính còn được gọi là hồi quy bình phương nhỏ nhất (OLS - ordinary least squares)
Đường hồi quy chỉ là một trong vô số các đường có thể vẽ được từ biểu đồ phân tán của X và Y.
3.1.2. Phương trình của đường hồi quy
Phương trình tuyến tính (hay còn gọi là regression line) có dạng như sau:

Trong đó:
-
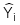 : Giá trị ước lượng của
: Giá trị ước lượng của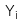 khi biết
khi biết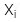
-
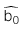 : Giá trị ước lượng của hệ số chặn
: Giá trị ước lượng của hệ số chặn -
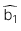 : Giá trị ước lượng của hệ số góc
: Giá trị ước lượng của hệ số góc
Lưu ý: Ký hiệu “^” ở trên các biến hay tham số để ám chỉ rằng đây là các giá trị dự đoán (predicted value).
a. Hệ số góc (slope coefficient)
Định nghĩa: mô tả sự thay đổi của Y khi thay đổi 1 đơn vị của X.
Công thức:
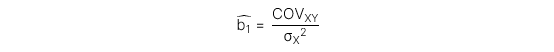
Diễn giải:
-
Hệ số góc > 0: thay đổi của biến độc lập sẽ cùng chiều với thay đổi của biến phụ thuộc
-
Hệ số góc < 0: thay đổi của biến độc lập sẽ ngược chiều với thay đổi của biến phụ thuộc
b. Hệ số chặn (intercept term)
Định nghĩa: chính là điểm giao giữa đường hồi quy và trục y
Công thức:
![]()
Trong đó:
-
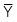 = Trung bình của biến Y
= Trung bình của biến Y -
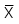 = Trung bình của biến X
= Trung bình của biến X
Diễn giải:
Hệ số chặn chính là giá trị ước lượng của biến phụ thuộc Y khi biến độc lập X = 0
3.2. Hồi quy cắt ngang và hồi quy chuỗi thời gian
Phân tích hồi quy sử dụng hai loại dữ liệu chính là cross-sectional data (dữ liệu của nhiều chủ thể tại một thời điểm) và time-series data (dữ liệu của một chủ thể trong một khoảng thời gian).
3.2.1. Hồi quy cắt ngang
Hồi quy cắt ngang (Cross-sectional regression) là hồi quy các quan sát X và Y tại cùng một thời điểm. Những quan sát này có thể là dữ liệu của các công ty, nhóm tài sản, quỹ đầu tư, quốc gia hay các chủ thể khác tùy vào mô hình hồi quy.
3.2.2. Hồi quy chuỗi thời gian
Hồi quy chuỗi thời gian (Time-series regression) là hồi quy sử dụng các quan sát từ nhiều thời điểm khác nhau cho cùng một chủ thể. Chủ thể ở đây có thể là một công ty, nhóm tài sản, quỹ đầu tư, quốc gia hay các chủ thể khác tùy thuộc vào mô hình hồi quy.
[LOS 10.b] Giải thích các giả định cơ bản của mô hình hồi quy tuyến tính đơn; mô tả cách các phần dư và các đồ thị phần dư chỉ ra liệu các giả định này có thể đã bị vi phạm hay không
Bốn giả định thông dụng đối với mô hình hồi quy bao gồm:
-
Linearity: Mối quan hệ giữa biến độc lập và biến phụ thuộc là mỗi quan hệ tuyến tính.
-
Homoskedasticity: Phương sai của phần dư đều bằng nhau đối với tất cả các quan sát.
-
Independence: Các biến không có tương quan với nhau.
-
Normality: Phần dư (residuals) theo phân phối chuẩn.
[LOS 10.c] Đo lường và diễn giải các đo lường sự phù hợp của mô hình và xây dựng và đánh giá các kiểm định cho sự phù hợp và cho giá trị tổng thể của hệ số hồi quy
1. Các thành phần cấu thành Total Sum of Squares (SST)
Biến động (variation) của biến phụ thuộc bao gồm phần biến động có thể giải thích được (explained variation) và phần biến động không thể giải thích được (unexplained variation), được thể hiện qua công thức:
SST = RSS + SSE
(Total variation = Explained variation + Unexplained variation)
Trong đó:
Total Sum of Squares (SST) đo lường tổng biến động của biến phụ thuộc, được thể hiện qua công thức:
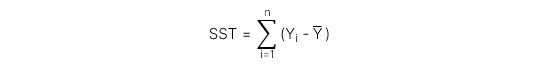
Regression sum of squares (RSS) đo lường phần biến động của biến phụ thuộc có thể giải thích được bởi biến độc lập, được thể hiện qua công thức:
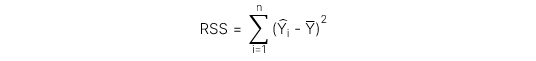
Sum of squared errors (SSE) đo lường phần biến động của biến phụ thuộc không thể giải thích được bởi biến độc lập, được thể hiện qua công thức:
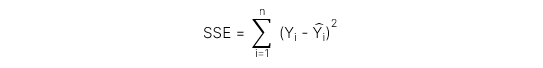
2. Coefficient of determination
Định nghĩa: Coefficient of determination (![]() ) là tỷ lệ phần trăm phần biến động của biến phụ thuộc được giải thích bởi biến độc lập. Công thức tính như sau:
) là tỷ lệ phần trăm phần biến động của biến phụ thuộc được giải thích bởi biến độc lập. Công thức tính như sau:

Diễn giải: ![]() càng cao cho thấy mô hình càng phù hợp.
càng cao cho thấy mô hình càng phù hợp.
3. F-test
F-test được sử dụng để kiểm định giả thuyết xem liệu hệ số góc của mô hình hồi quy có bằng 0 hay không. Lưu ý rằng F-test luôn là kiểm định giả thuyết một phía. F-test có 6 bước được trình bày như dưới đây.
-
Bước 1: Nêu giả thuyết
Giả thuyết cho hồi quy đa biến
![]() :
: ![]()
![]() : có ít nhất một hệ số góc khác 0
: có ít nhất một hệ số góc khác 0
Trong đó:
k = số lượng biến độc lập
Giả thuyết cho hồi quy đơn biến
![]() :
: ![]()
![]() :
: ![]()
-
Bước 2: Xác định giá trị thống kê kiểm định (test statistic)
Giá trị thống kê kiểm định (test statistic) cho F-test có công thức như sau. Hồi quy đơn biến chỉ có 2 phương sai nên k = 1 và như vậy ta có:
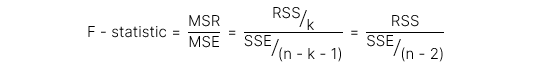
Trong đó, bậc tự do của tử và mẫu lần lượt như sau:
-
df (numerator) = k = 1
-
df (denominator) = n – k – 1 = n - 2
Tử số mean square regression (MSR) được tính cụ thể như sau:
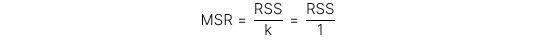
Trong đó: k = số lượng hệ số góc được ước lượng (hay số lượng biến độc lập)
- Mẫu số mean square error (MSE) được tính cụ thể như sau:
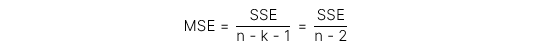
-
Bước 3: Xác định mức ý nghĩa (level of significant)
Mức ý nghĩa là dữ kiện đề bài cho, thông dụng nhất thường là 10%, 5% và 1%.
-
Bước 4: Xác định giá trị tới hạn (critical value) và nêu quy tắc ra quyết định
F-critical phụ thuộc vào mức ý nghĩa và bậc tự do của tử số và mẫu số. Từ đó tra bảng F-table cho kiểm định một phía để xác định F-critical value tương ứng.
Bác bỏ ![]() khi F-statistic > F-critical.
khi F-statistic > F-critical.
-
Bước 5: Tính toán tham số thống kê của mẫu
Tính toán F-statistic với công thức ở bước 2.
-
Bước 6: Ra quyết định về giả thuyết thống kê
Bác bỏ ![]() khi F-statistic > F-critical.
khi F-statistic > F-critical.
Không bác bỏ ![]() khi F-statistic < F-critical.
khi F-statistic < F-critical.
Diễn giải: Bác bỏ ![]() ngụ ý rằng biến độc lập và biến phụ thuộc có mối quan hệ tuyến tính có ý nghĩa thống kê.
ngụ ý rằng biến độc lập và biến phụ thuộc có mối quan hệ tuyến tính có ý nghĩa thống kê.
4. Kiểm định giả thuyết liên quan tới các giá trị tổng thể của hệ số hồi quy
4.1. Kiểm định giả thuyết cho hệ số góc
Sử dụng test statistic theo phân phối t để kiểm định giả thuyết về hệ số góc.
-
Bước 1: Nêu giả thuyết
![]() :
: 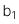 =
= 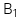 với
với ![]() :
: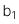 ≠
≠ 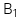
![]() :
: 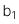 ≤
≤ 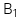 với
với ![]() :
: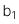 >
> 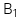
![]() :
: 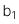 ≥
≥ 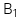 với
với ![]() :
: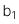 <
< 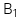
-
Bước 2: Xác định giá trị thống kê kiểm định (test statistic)
Test statistic cho t-test với bậc tự do df = n - 2 có công thức như sau:
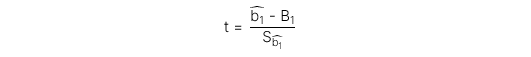
Trong đó:
-
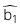 : Hệ số góc ước lượng
: Hệ số góc ước lượng -
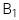 : Hệ số góc giả thuyết
: Hệ số góc giả thuyết -
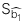 : Sai số chuẩn (Standard error) của hệ số góc
: Sai số chuẩn (Standard error) của hệ số góc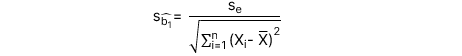
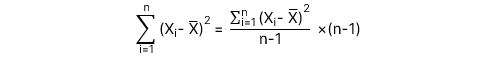
-
Bước 3: Xác định mức ý nghĩa (level of significance)
Mức ý nghĩa là dữ kiện đề bài cho, thông dụng nhất thường là 10%, 5% và 1%.
-
Bước 4: Xác định giá trị tới hạn (critical value) và nêu quy tắc ra quyết định
Dựa trên mức ý nghĩa, sử dụng t-table để xác định t-critical value
Bác bỏ ![]() khi t-statistic > + t-critical hoặc t-statistic < t-critical
khi t-statistic > + t-critical hoặc t-statistic < t-critical
-
Bước 5: Tính toán tham số thống kê của mẫu
Tính toán t-statistic theo công thức ở bước 2.
-
Bước 6: Ra quyết định về giả thuyết thống kê
Bác bỏ ![]() khi t-statistic > + t-critical hoặc t-statistic < t-critical và đưa ra kết luận phù hợp.
khi t-statistic > + t-critical hoặc t-statistic < t-critical và đưa ra kết luận phù hợp.
4.2. Kiểm định giả thuyết cho hệ số tương quan
Sử dụng test statistic theo phân phối t để kiểm định giả thuyết rằng liệu có sự tương quan (mối quan hệ tuyến tính) có ý nghĩa thống kê giữa biến độc lập và biến phụ thuộc hay không.
-
Bước 1: Nêu giả thuyết
![]() : ρ = 0 với
: ρ = 0 với ![]() : ρ ≠ 0
: ρ ≠ 0
![]() : ρ ≤ 0 với
: ρ ≤ 0 với ![]() : ρ > 0
: ρ > 0
![]() : ρ ≥ 0 với
: ρ ≥ 0 với ![]() : ρ < 0
: ρ < 0
-
Bước 2: Xác định giá trị thống kê kiểm định (test statistic)
Test statistic cho t-test với bậc tự do df = n – 2 có công thức như sau:
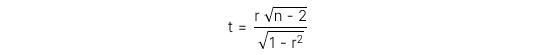
Trong đó:
-
r: hệ số tương quan của mẫu (Sample correlation)
-
n: số lượng quan sát của mẫu
-
Bước 3: Xác định mức ý nghĩa (level of significance)
Mức ý nghĩa là dữ kiện đề bài cho, thông dụng nhất thường là 10%, 5% và 1%.
-
Bước 4: Xác định giá trị tới hạn (critical value) và nêu quy tắc ra quyết định
Dựa trên mức ý nghĩa, sử dụng t-table để xác định t-critical value
Bác bỏ ![]() khi t-statistic > +t-critical hoặc t-statistic < −t-critical
khi t-statistic > +t-critical hoặc t-statistic < −t-critical
-
Bước 5: Tính toán tham số thống kê của mẫu
Tính toán t-statistic theo công thức ở bước 2.
-
Bước 6: Ra quyết định về giả thuyết thống kê
Bác bỏ ![]() khi t-statistic > +t-critical hoặc t-statistic < −t-critical và đưa ra kết luận phù hợp.
khi t-statistic > +t-critical hoặc t-statistic < −t-critical và đưa ra kết luận phù hợp.
4.3. Kiểm định giả thuyết của hệ số chặn (intercept)
Sử dụng test statistic theo phân phối t để kiểm định giả thuyết xem hệ số chặn có bằng một giá trị cụ thể nào không.
-
Bước 1: Nêu giả thuyết
![]() :
: 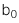 =
= 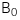 với
với ![]() :
: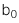 ≠
≠ 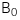
![]() :
: 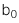 ≤
≤ 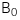 với
với ![]() :
: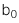 >
> 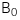
![]() :
: 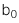 ≥
≥ 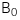 với
với ![]() :
: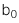 <
< 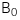
-
Bước 2: Xác định giá trị thống kê kiểm định (test statistic)
Test statistic cho t-test với bậc tự do df = n – 2 có công thức như sau:
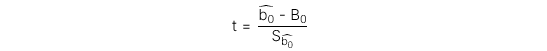
Trong đó:
-
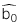 : Hệ số chặn ước lượng
: Hệ số chặn ước lượng -
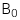 : Hệ số chặn giải thuyết
: Hệ số chặn giải thuyết -
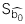 : Sai số chuẩn (Standard error) của hệ số chặn.
: Sai số chuẩn (Standard error) của hệ số chặn.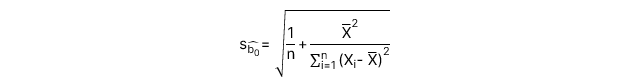
-
Bước 3: Xác định mức ý nghĩa (level of significance)
Mức ý nghĩa là dữ kiện đề bài cho, thông dụng nhất thường là 10%, 5% và 1%.
-
Bước 4: Xác định giá trị tới hạn (critical value) và nêu quy tắc ra quyết định
Dựa trên mức ý nghĩa, sử dụng t-table để xác định t-critical value
Bác bỏ ![]() khi t-statistic > +t-critical hoặc t-statistic < −t-critical
khi t-statistic > +t-critical hoặc t-statistic < −t-critical
-
Bước 5: Tính toán tham số thống kê của mẫu
Tính toán t-statistic theo công thức ở bước 2.
-
Bước 6: Ra quyết định về giả thuyết thống kê
Bác bỏ ![]() khi t-statistic > +t-critical hoặc t-statistic < −t-critical và đưa ra kết luận phù hợp.
khi t-statistic > +t-critical hoặc t-statistic < −t-critical và đưa ra kết luận phù hợp.
[LOS 10.d] Mô tả việc sử dụng phân tích phương sai (ANOVA) trong phân tích hồi quy, diễn giải kết quả ANOVA; đo lường và diễn giải sai số chuẩn của ước lượng trong một hồi quy tuyến tính đơn
1. Sai số chuẩn của ước lượng
Sai số chuẩn của ước lượng (Standard Error of Estimate - SEE) đo lường khoảng cách giữa các giá trị thực tế và giá trị ước lượng trong mô hình hồi quy của biến phụ thuộc. SEE có công thức tính như sau:
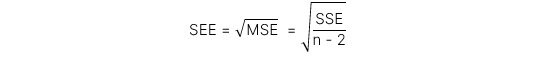
Diễn giải: SEE càng nhỏ thì mô hình càng phù hợp
2. Phân tích phương sai
Phân tích phương sai (Analysis of Variance - ANOVA) là quy trình thống kê được sử dụng để phân tích biến động của biến phụ thuộc.
|
Source of variation |
Degrees of Freedome |
Sum of Squares |
Mean Sum of Squares |
F-statistic |
|---|---|---|---|---|
|
Regression |
1 |
|
|
|
|
Error |
n - 2 |
|
|
|
|
Total |
n - 1 |
SST = RSS + SSE |
|
|
[LOS 10.e] Đo lường và diễn giải giá trị ước lượng cho biến phụ thuộc và khoảng tin cậy ước lượng dựa trên mô hình hồi quy tuyến tính ước tính và giá trị của biến độc lập
1. Giá trị ước lượng (Predicted value)
Giá trị ước lượng của biến phụ thuộc dựa trên:
-
Giá trị ước lượng của hệ số chặn và hệ số góc (
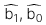 )
) -
Giá trị ước lượng của biến độc lập (
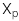 )
)
Công thức xác định giá trị ước lượng biến phụ thuộc của mô hình hồi qua đơn biến như sau:
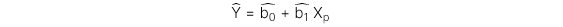
Trong đó:
-
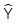 : Giá trị ước lượng của biến phụ thuộc
: Giá trị ước lượng của biến phụ thuộc -
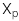 : Giá trị ước lượng của biến độc lập
: Giá trị ước lượng của biến độc lập -
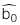 : Giá trị ước lượng của hệ số chặn
: Giá trị ước lượng của hệ số chặn -
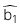 : Giá trị ước lượng của hệ số góc
: Giá trị ước lượng của hệ số góc
2. Khoảng tin cậy
Khoảng tin cậy (Confidence interval) là một khoảng giá trị xung quanh giá trị kỳ vọng, mà ta kỳ vọng xác suất nó bao hàm giá trị thực là 100(1-α)%, với α là mức ý nghĩa.
-
Bước 1: Ước lượng giá trị của Y
-
Bước 2: Chọn mức ý nghĩa (significant level)
-
Bước 3: Xác định giá trị tới hạn (critical value) và nêu quy tắc ra quyết định
-
Bước 4: Tính toán sai số chuẩn (standard error)
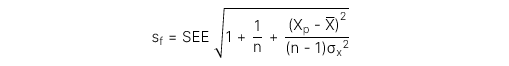
Trong đó:
SEE: Sai số chuẩn (Standard error) của ước lượng
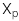 : Giá trị ước lượng của biến độc lập
: Giá trị ước lượng của biến độc lập
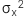 : Phương sai của biến độc lập
: Phương sai của biến độc lập
-
Bước 5: Tính toán khoảng tin cậy

[LOS 10.f] Mô tả các dạng hàm khác nhau của hồi quy tuyến tính đơn
Khi các giả định cho mối quan hệ tuyến tính không được tuân theo, việc biến đổi một hoặc cả hai biến có thể cho ra một mối quan hệ tuyến tính. Việc biến đổi phù hợp sẽ dựa trên mối quan hệ giữa hai biến. Cách biến đổi thông dụng thường là lấy log tự nhiên cho một hoặc cả hai biến. Có 3 mô hình hồi quy chính khi lấy log tự nhiên cho biến như sau.
1. Mô hình Log-lin
Biến phụ thuộc được đổi thành dạng log còn biến độc lập là tuyến tính.
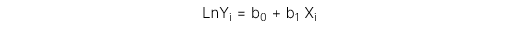
2. Mô hình Lin-log
Biến phụ thuộc là tuyến tính còn biến độc lập được đổi thành dạng log.
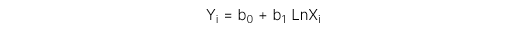
3. Mô hình Log-log
Cả biến phụ thuộc và biến độc lập là tuyến tính ở dạng log. Mô hình này có tên gọi khác là mô hình double-log.