Bài viết cung cấp cho người đọc kiến thức về Module 12 môn FI của chương trình CFA level I
I. Tính toán và giải thích độ lồi (convexity) và miêu tả điều chỉnh độ lồi (convexity adjustment); tính tỷ lệ phần trăm thay đổi giá của một trái phiếu đối với một sự thay đổi lợi tức cụ thể, dựa trên thời gian đáo hạn và độ lồi của trái phiếu
1. Độ lồi của trái phiếu (Bond convexity)
Mối quan hệ giữa trái phiếu và YTM là một đường cong võng xuống (convex curve).
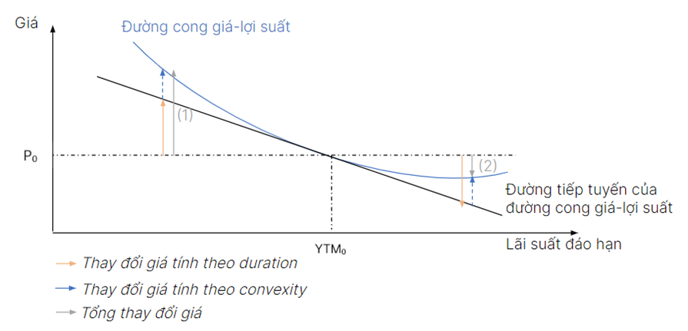
Việc sử dụng độ lồi (convexity) trong việc đo lường sự biến động giá có thể khắc phục nhược điểm của sử dụng thời gian đáo hạn bình quân (duration) trong việc đo lường độ nhạy của giá trái phiếu khi lãi suất thay đổi.
Annual convexity là thước đo cho độ lồi trái phiếu và có thể được tính toán xấp xỉ dựa trên công thức sau:
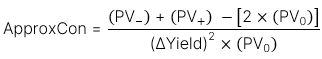
Sự thay đổi giá trái phiếu khi có sự thay đổi về YTM trường hợp xét thêm tác động độ lồi được thể hiện trong công thức dưới đây:
![]()
Trong đó:
-
Hiệu ứng bậc 1 (First order effect/Duration effect): Tác động của thời gian đáo hạn trung bình (duration effect) lên sự thay đổi giá trái phiếu khiến giá trái phiếu giảm (tăng) khi YTM tăng (giảm).
-
Hiệu ứng bậc 2 (Second order effect/Convexity adjustment): Tác động của điều chỉnh độ lồi (convexity adjustment) lên sự thay đổi giá trái phiếu luôn là tác động dương cho cả sự tăng/giảm của YTM.
2. Độ lồi tính theo giá trị tuyệt đối (Money convexity)
Money convexity đo lường hiệu ứng bậc 2 trên sự thay đổi tuyệt đối (tính theo đơn vị tiền tệ) của giá trái phiếu khi có sự thay đổi về lãi suất YTM.
![]()
Sự thay đổi quy về tiền mặt của giá trái phiếu trường hợp xét thêm tác động độ lồi được thể hiện trong công thức dưới đây:
![]()
3. Các yếu tố ảnh hưởng đến độ lồi
Các nhân tố khiến duration tăng cũng khiến convexity tăng. Tham khảo các yếu tố trong bảng dưới đây.
|
Yếu tố |
Chiều thay đổi của yếu tố |
Chiều thay đổi của độ lồi |
|
Kỳ hạn |
Tăng |
Tăng |
|
Lãi suất coupon |
Giảm |
Tăng |
|
Lãi suất đáo hạn (YTM) |
Giảm |
Tăng |
|
Độ phân tán của dòng tiền |
Tăng |
Tăng |
Lợi ích của việc có độ lồi trái phiếu cao hơn: Các trái phiếu có đường giá-lợi suất cong nhiều hơn sẽ ít nhạy cảm với lãi suất hơn các trái phiếu có đường giá-lợi suất cong ít hơn trong cả bối cảnh thị trường tăng và giảm → Ít rủi ro hơn cho nhà đầu tư.
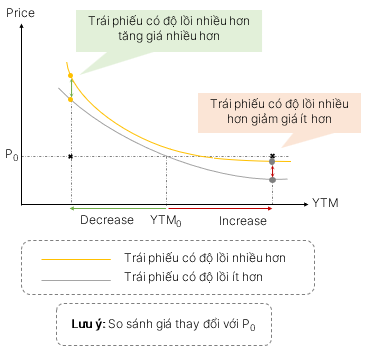
4. Độ lồi hiệu dụng của trái phiếu (Effective convexity)
Cũng tương tự như effective duration, effective convexity được sử dụng để đo lường tác động của “hiệu ứng bậc 2” của rủi ro lãi suất đối với trái phiếu đính kèm quyền chọn. Effective convexity của trái phiếu được tính toán theo công thức sau:
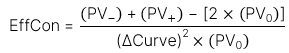
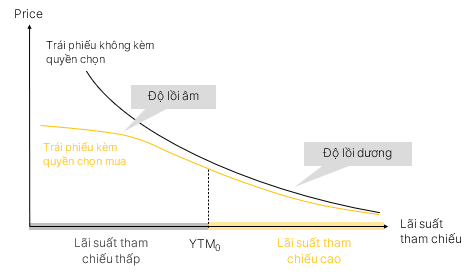
4.1. Độ lồi hiệu dụng của trái phiếu kèm quyền chọn mua (callable bond)
|
Lãi suất tham chiếu |
Độ lồi |
So sánh tác động của thay đổi lãi suất lên giá trái phiếu |
|
Thấp |
Độ lồi callable bond < 0 < Độ lồi straight bond (đường cong võng lên – concavity) |
Callable bond tăng giá < Straight bond tăng giá |
|
Cao |
Độ lồi callable bond > 0 (đường cong võng xuống, tương tự như straight bond) |
Callable bond giảm giá ≈ Straight bond giảm giá |
Point of inflection: Điểm mà độ lồi của trái phiếu kèm quyền chọn mua chuyển từ giá trị âm sang dương.
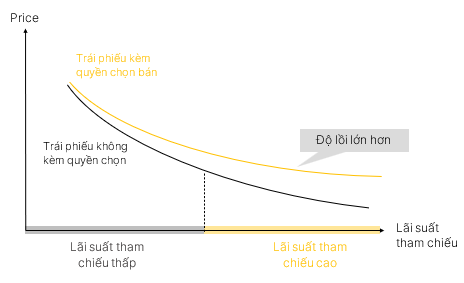
4.2. Độ lồi hiệu dụng của trái phiếu kèm quyền chọn bán (putable bond)
|
Lãi suất tham chiếu |
Độ lồi |
So sánh tác động của thay đổi lãi suất lên giá trái phiếu |
|
Thấp |
Độ lồi putable bond > 0 (đường cong võng xuống, tương tự như straight bond) |
Putable bond tăng giá ≈ Putable bond tăng giá |
|
Cao |
Độ lồi putable bond > Độ lồi straight bond > 0 |
Putable bond giảm giá < Straight bond giảm giá |
II. Tính toán thời gian đáo hạn bình quân của danh mục đầu mục và độ lồi (convexity) và giải thích hạn chế của các phương thức đo lường
Duration và convexity của một danh mục trái phiếu có thể được tính toán theo hai phương pháp sau. Mỗi phương pháp đều có ưu và nhược điểm riêng được trình bày trong bảng dưới đây.
|
|
Phương pháp 1 Weighted average of durations |
Phương pháp 2: Weighted average of time to receipt cash flows |
|
Mô tả |
→ Tính giá trị bình quân gia quyền của duration. |
→ Tính thời gian bình quân gia quyền để nhận được tổng dòng tiền tích lũy.
|
|
Ưu điểm |
Tính toán đơn giản hơn, thường được sử dụng bởi các nhà quản trị danh mục trái phiếu |
Đúng về mặt lý thuyết |
|
Nhược điểm |
Phương pháp này giả định rằng đường cong lãi suất dịch chuyển song song → Giả định không đúng trong thực tế, vì danh mục trái phiếu bao gồm rất nhiều trái phiếu khác nhau với các kỳ hạn khác nhau, mức độ rủi ro tín dụng và quyền chọn khác nhau. |
|
-1.png?height=120&name=SAPP%20logo%20m%E1%BB%9Bi-01%20(1)-1.png)