[Level 1] Quantitative Methods
      Quay lại trang chủ
      1. SAPP Knowledge Base
      2. Tự học CFA Level I (Chartered Financial Analyst)
      3. [Level 1] Quantitative Methods

      [Tóm tắt kiến thức quan trọng] Module 3: Statistical Measures of Asset Returns

      Bài viết cung cấp cho người đọc kiến thức về Module 3 môn Quantitative Methods của chương trình CFA level I

      [Pre.i,ii] Xác định và phân loại các kiểu dữ liệu; mô tả cách tổ chức dữ liệu cho phân tích định lượng

      1. Khái niệm và phân loại dữ liệu

      1.1. Khái niệm: Dữ liệu có thể được định nghĩa là một tập hợp các số, ký tự, từ và văn bản cũng như hình ảnh, âm thanh và video dưới định dạng thô hoặc có tổ chức để đại diện cho sự thật hoặc thông tin

      1.2. Phân loại dữ liệu theo quan điểm thống kê

      Theo quan điểm thống kê, CFA phân ra thành 2 loại chính bao gồm:

      Dữ liệu định lượng (Quantitative data): Trong dữ liệu định lượng, CFA lại chia nhỏ ra thành 2 nhóm, bao gồm:

      • Discrete data: Các dữ liệu số được lấy từ quá trình đếm và do đó được giới hạn ở số lượng giá trị hữu hạn.

      • Continuous data: Dữ liệu có thể được đo và có thể nhận bất kỳ giá trị số nào trong một phạm vi giá trị được chỉ định và do đó không giới hạn với số lượng giá trị hữu hạn.

      Dữ liệu định tính (Qualitative data): Trong dữ liệu định tính, CFA lại chia nhỏ ra thành 2 nhóm, bao gồm:

      • Nominal data: Các giá trị phân loại không thể được sắp xếp theo thứ tự hợp lý.

      • Ordinal data: Các giá trị phân loại có thể được xếp hạng một cách hợp lý.

      1.3. Phân loại dữ liệu theo cách thu thập dữ liệu

      Theo cách phân loại này, dữ liệu sẽ được phân thành 3 loại như sau:

      • Time Series Data: Các quan sát của một biến được thực hiện trong một khoảng thời gian tại các khoảng thời gian cụ thể và đều nhau.

      • Cross-sectional data: Một mẫu quan sát của nhiều biến được lấy tại một thời điểm duy nhất.

      • Panel Data: Quan sát theo thời gian của cùng một đặc điểm cho nhiều biến.

      1.4. Phân loại dữ liệu theo cấu trúc tổ chức

      Theo cách phân loại này, dữ liệu sẽ được phân thành 2 loại như sau:

      • Structured data: Dữ liệu đã được xử lý và tổ chức lại theo form được xác định trước, thường là với mô hình lặp lại.

      • Unstructured data: Dữ liệu không tuân theo bất kỳ hình thức có tổ chức thông thường nào.

      [Pre.iii] Giải thích tần suất và các phân phối liên quan

      Phân phối tần suất (frequency distribution) có bộ dữ liệu được xây dựng bằng cách kiểm đếm các quan sát của một biến theo các giá trị/ nhóm riêng biệt hoặc bằng cách kiểm đếm các giá trị của một biến số thành một tập hợp các giá trị được sắp xếp hợp lý.

       

      [Pre.iv] Diễn giải về bảng tương quan

      Bảng tương quan (contingency table) là một định dạng bảng hiển thị phân phối tần số của hai hoặc nhiều biến phân loại đồng thời.

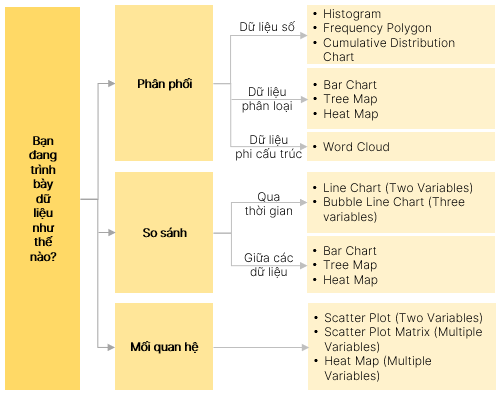
      [Pre.v] Mô tả các cách trực quan hóa dữ liệu và ứng dụng của từng loại biểu đồ cụ thể

      Các loại biểu đồ mô tả dữ liệu phổ biến:

      • Histogram

      • Frequency polygon

      • Bar chart

      • Tree map

      • Word cloud

      • Line chart

      • Scatter Plot

      • Heat Map

      [Pre.vi] Mô tả cách chọn biểu đồ để trực quan hóa và trình bày dữ liệu

      [LOS 3.a] Đo lường và diễn giải các thông số đo lường của xu hướng trung tâm và vị trí

      1. Arithmetic Mean - Giá trị trung bình

      Định nghĩa : Tổng các giá trị của các quan sát chia cho số lượng quan sát.

      Công thức đối với tổng thể:

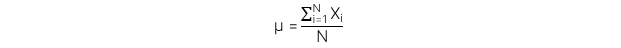
      Công thức đối với mẫu:

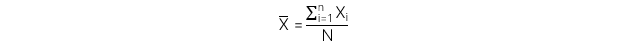
      Lưu ý: Nhược điểm của Arithmetic mean là rất dễ bị ảnh hưởng bởi các outliers. Để khắc phục hạn chế trên, có 3 cách để lựa chọn xử lý các outliers.

      • Cách 1: Sử dụng dữ liệu mà không cần điều chỉnh nếu các outliers phản ánh đúng thực tế.

      • Cách 2: Xóa tất cả outliers.

      • Cách 3: Thay thế các outliers bằng giá trị khác.

      2. Median - Trung vị: Điểm giữa của tập dữ liệu khi dữ liệu được sắp xếp theo thứ tự tăng dần hoặc giảm dần.

      3. Mode - Yếu vị: Giá trị xuất hiện nhiều nhất trong tập dữ liệu. Một tập dữ liệu có thể có nhiều hơn một mode hoặc thậm chí không có mode.

      4. Đo lường điểm phân vị và minh họa các điểm phân vị bằng hình ảnh

      Quantile

      Phân vị (quantile) là các điểm cắt/điểm mốc chia một khoảng phân phối xác suất ra thành các khoảng với xác suất giống nhau, từ đó sẽ xác định được một tỷ lệ nhất định của lượng dữ liệu nằm dưới mỗi điểm mốc này.

      Công thức

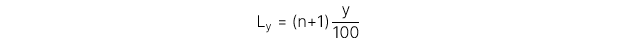
      Trong đó:

      • y = Điểm phần trăm để phân chia phân phối.

      • n = Số lượng điểm dữ liệu được sắp xếp theo thứ tự tăng dần.

      [LOS 3.b] Đo lường và diễn giải các thông số của xu hướng phân tán

      1. Range

      Phạm vi là sự chênh lệch giữa giá trị lớn nhất và nhỏ nhất trong bộ dữ liệu.

      Công thức: Range = Maximum value − Minimum value.

      2. Mean absolute deviation (MAD)

      Là đại lượng được tính bằng cách lấy tổng các giá trị tuyệt đối của độ lệch giữa kết quả quan sát và số bình quân, chia cho số kết quả quan sát.

      Công thức

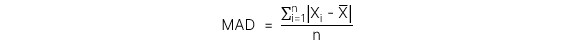
      3. Variance

      Giá trị trung bình của độ lệch bình phương so với trung bình số học hoặc từ giá trị kỳ vọng ​​của phân phối.

      Công thức

      • Phương sai của mẫu:

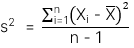
      • Phương sai của tổng thể:

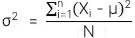
      4. Standard deviation

      Căn bậc hai dương của phương sai.

      4.1. Công thức

      • Độ lệch chuẩn của mẫu:

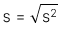
      • Độ lệch chuẩn của tổng thể:

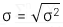
      4.2. Đo lường và diễn giải độ lệch chuẩn dưới

      Target downside deviation

      Thước đo rủi ro của việc thấp hơn một mục tiêu nhất định.

      Công thức

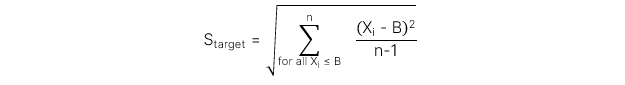
      5. Coefficient of variation (CV)

      Tỉ số giữa độ lệch chuẩn của một tập hợp các quan sát với giá trị trung bình của chúng.

      Ý nghĩa: Một đồng rủi ro được đảm bảo bởi bao nhiêu đồng lợi nhuận.

      Công thức

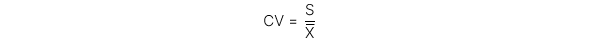
      [LOS 3.c] Cách đo lường và diễn giải về độ lệch, độ nhọn và hệ số tương quan để trả lời các vấn đề về đầu tư

      1. Diễn giải về độ lệch

      Độ lệch (skewness) là thước đo đề cập đến độ lệch của phân phối so với phân phối chuẩn.

      • Skewness = 0: Đối xứng (symmetrical) → Mean = Median = Mode.

      • Skewness > 0: Lệch phải (positively skewed) → Mean > Median > Mode.

      • Skewness < 0: Lệch trái (negatively skewed) → Mean < Median < Mode.

      2. Diễn giải về độ nhọn

      Độ nhọn (kurtosis) là thước đo mức độ nhọn của một phân phối mà tại đó phân phối này nhọn hơn (more peaked) hay ít nhọn hơn (less peaked) so với phân phối chuẩn.

      • Kurtosis = 3 → Mesokurtic: Mô tả một phân phối có cùng độ nhọn với phân phối chuẩn.

      • Kurtosis > 3 → Leptokurtic: Mô tả một phân phối có đỉnh nhọn hơn phân phối chuẩn.

      • Kurtosis < 3 → Platykurtic: Mô tả phân phối có đỉnh ít nhọn hơn phân phối chuẩn.

      3. Diễn giải hệ số tương quan giữa hai biến

      Hệ số tương quan (correlation) đo lường mối quan hệ tuyến tính giữa hai biến. Trong đó:

      • Hệ số tương quan thuận thể hiện rằng hai biến số có xu hướng di chuyển cùng nhau.

      • Hệ số tương quan nghịch thể hiện rằng hai biến số có xu hướng di chuyển ngược chiều nhau.

      • Phạm vi hệ số tương quan đi từ -1 đến 1.

      Công thức hệ số tương quan của mẫu:

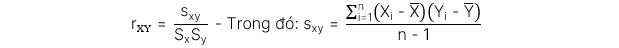
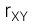      • = 0 → Không có mối quan hệ tuyến tính nào giữa X và Y

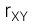      • = 1 →  Mối quan hệ tuyến tính thuận hoàn hảo giữa X và Y.

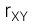      • = -1 →  Mối quan hệ tuyến tính nghịch hoàn hảo giữa X và Y.