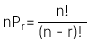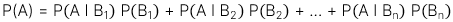[Level 1] Quantitative Methods
      Quay lại trang chủ
      1. SAPP Knowledge Base
      2. Tự học CFA Level I (Chartered Financial Analyst)
      3. [Level 1] Quantitative Methods

      [Tóm tắt kiến thức quan trọng] Module 4: Probability Trees and Conditional Expectations

      Bài viết cung cấp cho người đọc kiến thức về Module 4 môn Quantitative Methods của chương trình CFA level I

      [Pre.i] Định nghĩa biến ngẫu nhiên, kết quả và sự kiện

      Biến ngẫu nhiên (random variable) là một giá trị bằng số, thể hiện kết quả của một phép thử ngẫu nhiên.

      Kết quả (outcome) là các giá trị có thể có của một biến ngẫu nhiên.

      Biến cố (event) có thể là một kết quả hoặc một tập hợp nhiều kết quả.

      Xác suất (probability) của một biến cố là % tượng trưng cho khả năng có thể xảy ra biến cố đó trong một phép thử liên quan.

       

      [Pre.ii] Xác định hai đặc điểm quan trọng của xác suất, bao gồm biến cố xung khắc và hệ biến cố đầy đủ; so sánh xác suất thực nghiệm, chủ quan và tiên nghiệm

      Các đặc tính cơ bản của xác suất:

      • P(A): Xác suất xảy ra biến cố A (0 ≤ P(A) ≤ 1).

      • Biến cố xung khắc (mutually exclusive events): Mô tả hai hoặc nhiều biến cố không thể xảy ra đồng thời.

      • Hệ biến cố đầy đủ (exhaustive events): Các sự kiện phải bao gồm tất cả các kết quả có thể xảy ra.

      • Tổng các xác suất của bất kỳ tập hợp nào của biến cố xung khắc và biến cố đầy đủ đều bằng 1.

      Có 2 trường phái xác suất là xác suất chủ quan và xác suất khách quan. Trong xác suất khách quan, cũng chia ra 2 trường phái là xác suất thực nghiệm (empirical probability) và xác suất tiên nghiệm (priori probability). Trong đó:

      • Xác suất chủ quan (subjective probability) là phán đoán của cá nhân.

      • Xác suất thực nghiệm (empirical probability) là xác suất được xác định bằng cách phân tích dữ liệu trong quá khứ.

      • Xác suất tiên nghiệm (priori probability) là xác suất được xác định dựa trên dữ liệu quan sát và thực nghiệm.

      [Pre.iii] Mô tả xác suất của một sự kiện dưới dạng Odds for E và Odds Against E

      Odd là tỉ lệ giữa xác suất xảy ra 1 sự kiện so với xác suất không xảy ra sự kiện đó.

      1. Odds for

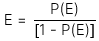
      2. Odds against

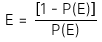
      Trong đó:

      • P(E) là xác suất xảy ra sự kiện đó.

      [Pre.iv] Đo lường và diễn giải xác suất có điều kiện

      Xác suất có điều kiện và xác suất vô điều kiện

      Xác suất vô điều kiện (unconditional probability) là xác suất xảy ra của một biến cố nhất định, không phụ thuộc vào sự xảy ra của biến cố nào trước/sau đó.

      Xác suất có điều kiện (conditional probability) là xác suất của một sự kiện xảy ra với điều kiện một sự kiện khác xảy ra. Công thức tính xác suất có điều kiện như sau:

      P (A I B) = P(AB) / P(B)

      Trong đó:

      P (A I B): Xác suất của sự kiện A với điều kiện rằng sự kiện B xảy ra.

      P(AB): Xác suất khi sự kiện A và B cùng xảy ra.

      P (B): Xác suất xảy ra sự kiện B

       

      [Pre.v] So sánh và đối chiếu các sự kiện phụ thuộc và độc lập

      Sự kiện độc lập (Independent events): Một sự kiện được xem là độc lập khi và chỉ khi sự xuất hiện của một sự kiện này không ảnh hưởng đến xác suất xuất hiện của sự kiện kia. 

      P(A|B) = P(A) hoặc P(B|A) = P(B)

      Sự kiện phụ thuộc (Dependent events): Các sự kiện không thỏa mãn được yêu cầu của sự kiện độc lập là các sự kiện phụ thuộc.

       

      [Pre.vi] Đo lường xác suất với quy tắc cộng, quy tắc nhân và quy tắc tổng hợp xác suất

      1. Quy tắc cộng

      • P(A or B) = P(A) + P(B) – P(AB)

      • Đối với các biến cố xung khắc: P(A or B) = P(A) + P(B)

      2. Quy tắc nhân

      • P(AB) = P(A I B) x P(B) = P(B I A) x P(A)

      • Đối với các biến cố độc lập: P(AB) = P(A) x P(B)

      3. Quy tắc tổng hợp xác suất

      [LOS 4.a] Tính toán và giải thích giá trị kỳ vọng, phương sai và độ lệch chuẩn của các biến ngẫu nhiên

      1. Giá trị kỳ vọng (Expected value): Là trung bình công có trọng số xác suất của các kết quả đầu ra có thể xảy ra của biến ngẫu nhiên.

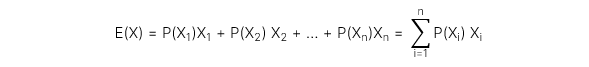
      2. Phương sai (Variance): Là giá trị kỳ vọng của bình phương độ lệch của các kết quả đầu ra và giá trị kỳ vọng của biến ngẫu nhiên.

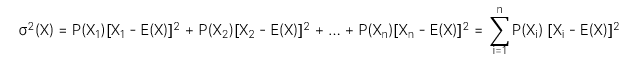
      3. Độ lệch chuẩn (Standard deviation): Là căn bậc hai dương của phương sai của biến ngẫu nhiên.

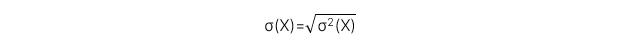
      4. Diễn giải cây xác suất và ý nghĩa ứng dụng của nó

      Sơ đồ cây (Tree diagram) có thể đại diện cho một loạt các sự kiện độc lập hoặc xác suất có điều kiện. Mỗi nút (node) trên sơ đồ đại diện cho một sự kiện và được liên kết với xác suất của sự kiện đó.
      Ứng dụng cơ bản của cây xác suất:

      • Sơ đồ cây là một cách thể hiện sự kết hợp của hai hoặc nhiều sự kiện.
      • Mỗi nhánh sẽ gồm kết quả và xác suất xảy ra kết quả đó.

      [LOS 4.c] Đo lường và diễn giải công thức Bayes

      1. Công thức Bayes

      2. Diễn giải:

      Khi chúng ta đưa ra quyết định liên quan đến đầu tư, các quan điểm mà ban đầu dựa trên kinh nghiệm và kiến thức của chúng ta, có thể bị thay đổi hoặc xác nhận bằng những quan sát mới

      → Công thức Bayes là một công cụ sử dụng để điều chỉnh quan điểm của chúng ta khi chúng ta đối mặt với thông tin mới.

       

      [Pre.vii] Xác định phương pháp thích hợp nhất để giải một bài toán đếm cụ thể và phân tích các bài toán đếm bằng cách sử dụng các khái niệm giai thừa, tổ hợp và chỉnh hợp

      Các công thức đếm

      • Giai thừa (Factorial): n! = n(n – 1)(n – 2)...1

      • Đa thức (Labeling):

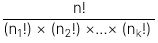
      • Tổ hợp (Combination):

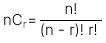
      • Chỉnh hợp (Permutation):