[Tóm tắt kiến thức quan trọng] Module 5: Portfolio Mathematics

Bài viết cung cấp cho người đọc kiến thức về Module 5 môn Quantitative Methods của chương trình CFA level I

[LOS 5.a,b] Đo lường và diễn giải giá trị kỳ vọng, phương sai, độ lệch chuẩn, hiệp phương sai và hệ số tương quan của các lợi nhuận của tài sản trong danh mục đầu tư

1. Expected Return (Lợi nhuận dự kiến)

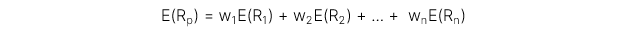
2. Covariance (Tính toán dựa trên dữ liệu xác suất)

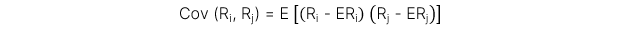
3. Correlation (Hệ số tương quan)

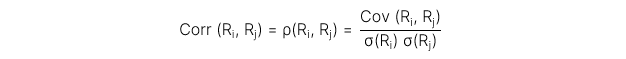
4. Variance (Phương sai)

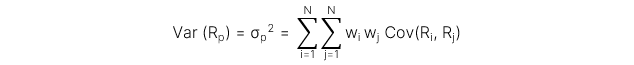
5. Standard Deviation (Độ lệch chuẩn)

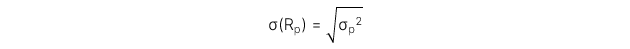
[Pre.i] Xác định phân phối xác suất; so sánh và đối chiếu giữa biến ngẫu nhiên rời rạc và liên tục, bao gồm các hàm xác suất của chúng

1. Biến ngẫu nhiên - Random Variables

Một giá trị bằng số, thể hiện kết quả của một phép thử ngẫu nhiên. Random Variables được chia thành 2 loại:

• Discrete random variables: Số lượng kết quả có thể xảy ra là hữu hạn và tạo thành một tập hợp hữu hạn đếm được.

• Continuous random variables: Số lượng kết quả có thể xảy ra là vô hạn, ngay cả khi tồn tại giới hạn dưới và giới hạn trên.

2. Hàm xác suất - Probability Function

Phân phối xác suất cho biết xác suất của các kết quả có thể có của một biến ngẫu nhiên.

• Biểu thị dưới dạng: p(x), là xác suất biến ngẫu nhiên X có giá trị x hoặc p(x) = P(X = x).

• 0 ≤ p(x) ≤1.

• Tổng tất cả p(x) luôn bằng 1.

[Pre.ii] Tính toán và giải thích xác suất của một biến ngẫu nhiên dựa trên hàm phân phối xác suất tích lũy của biến này

Hàm phân phối lũy kế - Cumulative distribution function

Xác định xác suất để một biến ngẫu nhiên, X, nhận một giá trị bằng hoặc nhỏ hơn một giá trị cụ thể, x.

Ký hiệu: F(x) = P(X ≤ x).

[Pre.iii] Mô tả các xác suất của một biến ngẫu nhiên đồng nhất rời rạc; tính toán và diễn giải các xác suất dựa trên hàm phân phối đồng nhất rời rạc của biến này

Phân phối đồng nhất rời rạc (Discrete uniform distribution)

Là phân phối xác suất mà khả năng xuất hiện của các kết quả là như nhau.

Đặc điểm:

• p(1) = p(2) = p(3) = ... = p(n)

• F(x) = P(X ≤ x)

[Pre.iv] Mô tả phân phối đồng nhất liên tục; tính toán và diễn giải các xác suất dựa trên hàm phân phối đồng nhất liên tục

Phân phối đồng nhất liên tục (Continuous uniform distribution)

Là phân phối xác suất được xác định trong một phạm vi kéo dài giữa một số giới hạn dưới, a và một số giới hạn trên, b, dùng làm tham số của phân phối.

Hàm mật độ xác suất:

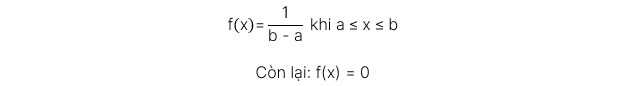
Hàm phân phối xác suất lũy kế:

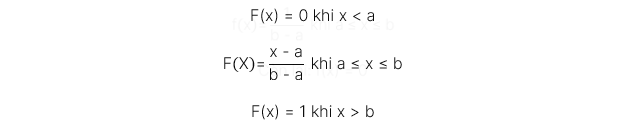
[Pre.v] Mô tả các thuộc tính của biến ngẫu nhiên Bernoulli và biến ngẫu nhiên nhị thức; tính toán và giải thích các xác suất dựa trên hàm phân phối nhị thức

Binomial distribution:

Phép thử Bernoulli là một thử nghiệm với hai kết quả duy nhất là thất bại và thành công.

Xác suất đạt x lần thành công trong n phép thử có công thức như sau:

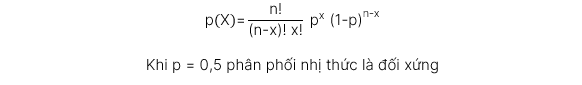
Số phép thử thành công kỳ vọng trong n phép thử X = E(X) = n x p.

Phương sai của biến ngẫu nhiên nhị thức X = n x p x (1-p).

[Pre.vi] Giải thích các đặc tính chính của phân phối chuẩn

1. Các đặc tính chính của phân phối chuẩn:

• Phân phối được xác định bởi 2 tham số là giá trị trung bình, μ và phương sai,

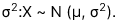
• Skewness = 0.

• Kurtosis = 3 và Excess kurtosis = 0

• Xác suất của các giá trị nhận được của X càng nằm xa giá trị trung bình sẽ càng nhỏ nhưng không nhận giá trị 0 (tiệm cận 0) với X nhận giá trị từ (-∞; +∞).

2. So sánh giữa phân phối đa biến và phân phối đơn biến; giải thích vai trò của hệ số tương quan trong phân phối chuẩn đa biến

Định nghĩa:

• Phân phối đơn biến (Univariate distribution): Mô tả các xác suất của một biến ngẫu nhiên duy nhất.

• Phân phối đa biến (Multivariate distribution): Mô tả các xác suất cho một nhóm các biến ngẫu nhiên có liên quan.

Đặc điểm chính của phân phối đa biến

Phân phối đa biến có ý nghĩa khi sự biến thiên của mỗi biến ngẫu nhiên trong nhóm theo một cách nào đó phụ thuộc vào hành vi của những biến khác.

Bộ ba tham số dùng để xác định phân phối chuẩn đa biến cho lợi nhuận của n tài sản bao gồm:

• Giá trị trung bình: có n giá trị trung bình của biến lợi nhuận

• Phương sai: có n giá trị phương sai của biến lợi nhuận

• Hệ số tương quan: có 0.5*n*(n-1) cặp hệ số tương quan tương ứng.

[Pre.vii] Tính toán xác suất để một biến ngẫu nhiên có phân phối chuẩn nằm trong một khoảng nhất định

Khoảng tin cậy (Confidence intervals) của phân phối chuẩn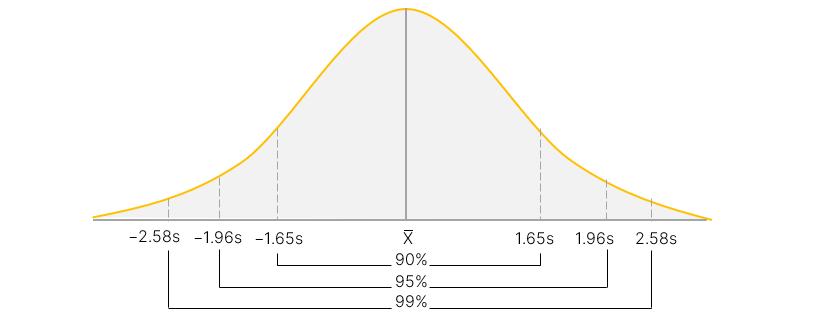

• Khoảng tin cậy 90% cho X là X - 1,65 × độ lệch chuẩn đến X + 1,65 × độ lệch chuẩn.

• Khoảng tin cậy 95% cho X là X - 1,96 × độ lệch chuẩn đến X + 1,96 × độ lệch chuẩn.

• Khoảng tin cậy 99% cho X là X - 2,58 × độ lệch chuẩn đến X + 2,58 × độ lệch chuẩn.

[Pre.viii] Giải thích cách chuẩn hóa một biến ngẫu nhiên; tính toán và giải thích các xác suất bằng cách sử dụng phân phối chuẩn tắc

Để chuẩn hóa một quan sát từ phân phối chuẩn nhất định (X), giá trị z-value của quan sát (Z) phải được tính:

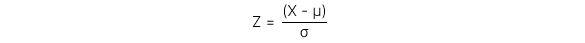
Trong đó:

• X ~ N (μ,)

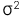• Z ~ N (0,1)

[LOS 5.c] Định nghĩa rủi ro tổn thất; tính toán chỉ số SFR; xác định danh mục đầu tư tối ưu bằng cách sử dụng Roy’s safety-first criterion

Shortfall risk: Xác suất mà giá trị danh mục đầu tư hoặc lợi nhuận sẽ giảm xuống dưới một mục tiêu cụ thể (hoặc lợi tức chấp nhận tối thiểu) trong một khoảng thời gian nhất định.

Roy’s safety - first: Danh mục đầu tư tối ưu là danh mục đầu tư giảm thiểu rủi ro thiếu hụt hoặc tối đa hóa tỷ lệ an toàn trên hết của Roy, trong đó:

Công thức:

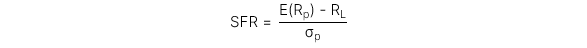
(RL: threshold return level, là mức tối thiểu có thể chấp nhận được)

Lưu ý: Tỷ lệ an toàn càng cao thì danh mục đầu tư càng tối ưu.