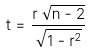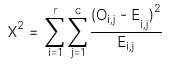[Tóm tắt kiến thức quan trọng] Module 9: Parametric and Non-parametric Tests of Independence

Bài viết cung cấp cho người đọc kiến thức về Module 9 môn Quantitative Methods của chương trình CFA level I

[LOS 9.a,b] Giải thích kiểm định tham số và kiểm định phi tham số khi tiến hành kiểm định hệ số tương quan; Giải thích kiểm định tính độc lập của dữ liệu dựa trên bảng tương quan

1. So sánh và đối chiếu các kiểm định tham số và phi tham số

Kiểm định tham số (Parametric tests): Bao gồm ít nhất một trong hai đặc điểm sau:

• Nó liên quan đến các tham số hoặc xác định các tính năng của một bản phân phối.

• Nó tạo ra một tập hợp các giả định xác định.

Kiểm định phi tham số (Non-parametric tests): Là phép thử không liên quan đến một tham số và chỉ đưa ra một tập hợp các giả định tối thiểu liên quan đến tổng thể.

2. Các tình huống khi nào nên nên sử dụng các bài kiểm định phi tham số

Kiểm định phi tham số được sử dụng khi:

• Dữ liệu không đáp ứng các giả định về phân phối.

• Có những tham số ngoại lai.

• Dữ liệu được đưa ra theo cấp bậc hoặc sử dụng thang thứ tự.

• Các giả thuyết kiểm định không liên quan đến một tham số.

3. Giải thích kiểm định tham số và kiểm định phi tham số khi tiến hành kiểm định hệ số tương quan; Giải thích kiểm định tính độc lập của dữ liệu dựa trên bảng tương quan

Áp dụng 6 bước cơ bản của kiểm định để đánh giá thống kê liên quan. Quy trình cụ thể bao gồm như sau:

• Bước 1: Nêu giả thuyết

• Bước 2: Xác định thống kê thử nghiệm thích hợp

• Bước 3: Chỉ định mức ý nghĩa

• Bước 4: Phát biểu quy tắc quyết định

• Bước 5: Thu thập dữ liệu và tính toán thống kê thử nghiệm

• Bước 6: Đưa ra quyết định liên quan đến giả thuyết

Nội dung bài học trong Module này bao gồm các kiểm định sau: